一般人のためのプリュッカー座標系 パート4 応用編

このブログポストは、Lionel Brits氏の Plücker Coordinates for the Rest of Us - Part 4 - Applications(2001)を、原著者の許可を得て翻訳・公開したものです。全ての権利は、原著者にあります。

プリュッカー座標系の基本的な性質

全てのプリュッカー座標が、$$R^3$$に関して対応する直線が必ずあるわけではない。最初の表記方法で書くところの$$L_U={\vec{U_1}:\vec{U_2}}$$で三次元空間に対応する直線が存在する条件式は次のようになる。

$$\vec{U_1}\cdot\vec{U_2}=0$$

$$\vec{U_1}\neq0$$である(直線は方向を持たなくてはならない)から、$$\vec{U_2}\neq0$$であると思うかもしれない(直線が原点を通過しないとすれば。$$\vec{U_2}=\vec{U}\times\vec{P}$$を思い出そう)。直線は原点を通過するかもしれないので、このチェックは三次元空間で直線ではないものを除外するだけで、三次元空間の直線であると保証するものではない。二つ目にでてきた表現方法では、次の時に三次元空間で直線が存在できる。

$$\Pi\odot\Pi=0$$

さらに、二つのプリュッカー座標$$L_U={\vec{U_1}:\vec{U_2}}$$と$$L_V={\vec{V_1}:\vec{V_2}}$$は次の時に同じ直線となる。

$$L_U=cL_v$$

$$c>0;c\in R^3$$であれば同じ向きの同じ直線に、$$c<0;c\in R^3$$であれば逆の向きの直線になる。$$L_U={\vec{U_1}:\vec{U_2}}$$と$$L_V={\vec{V_1}:\vec{V_2}}$$は、$$\vec{U_1}\cdot\vec{V_1}=0$$であれば垂直に、 $$\vec{U_1}\cdot\vec{V_1}=||\vec{U}||||\vec{V}||$$であれば平行になる。これらの点はプリュッカー座標が基づいている幾何から当然の帰結だ。

面と直線の交差

原点から$$d$$だけ離れている面の方向が$$N$$の平面の式を思い出そう。平面上の位置$$P$$の集合は、次の事を満たす。

$$N \cdot P=d$$

平面$$A$$と、直線$$L={\vec{U_1}:\vec{U_2}}$$について、この二つの斉次座標での交差は次のようになる

$$(U_2\times N - dU_1 : U_1 \cdot N)$$

デカルト座標系では次のように表される

$$\cfrac{U_2 \times N - dU_1}{U_1 \cdot N}$$

面と面の交差

面Aと面Bに関して、プリュッカー座標系での交差は次のようになる。

$$L_{AB} = {N_A \times N_A:d_B N_A - d_A N_B }$$

(訳注: 面と面の交差は直線になるので、プリュッカー座標で表現できる)

レイとポリゴンの交差、レイと凸包の交差

プリュッカー座標の私にとって最も魅力的な性質は、レイとポリゴンの交差判定[2]が簡単になることだった。ポリゴン上の全てのエッジをプリュッカー表現(頂点を全て同じ順列になるようにする)にすれば、レイと各エッジの置換された内積を全てのエッジに対して行うことで、ポリゴンに対して交差するか否かを決定できる。ポリゴンを通過したレイに関して、全ての積の符号は同じでなくてはならない(もしくは一つか二つの積が0で、その他の積の符号が同じ場合)。次の図では、交差しているレイの周りのエッジは反時計周りの向きだ。

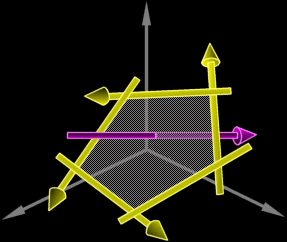
line_triangle

三角形や四角形と交差していたら、交差位置の計算ができる。$$L_0$$、$$L_1$$、$$L_2$$のエッジを持つ三角形で、$$L_n$$はn番目の頂点の反対側のエッジとする。レイ$$L_R$$と、$$L_0$$、$$L_1$$、$$L_2$$との積は、それぞれ$$\omega_0$$、$$\omega_1$$、$$\omega_2$$となる。それぞれの正負が一致するとき、交差していることになる。それらは、交差位置の正規化されていない重心座標であることがわかる。正規化の係数$$v=\omega_0+\omega_1+\omega_2$$を用いて正規化した重心座標は次のようになる。

$$a_0=\cfrac{\omega_0}{v}$$, $$a_1=\cfrac{\omega_1}{v}$$, $$a_2=\cfrac{\omega_2}{v}$$.

デカルト座標系での交差位置は頂点$$\vec{V_0}$$、$$\vec{V_1}$$、$$\vec{V_2}$$の一次結合で表される。交差位置$$\vec{Q}$$は次のようになる。

$$\vec{Q}=a_0\vec{V_0}+a_1\vec{V_1}+a_2\vec{V_2}$$

同じやり方で、レイ同士の交差、凸包(例えば立方体)の交差判定に拡張できる。レイがボリュームに交差するには、ボリュームの一つ以上の面に交差する必要がある。レイとポリゴンの交差判定はエッジが面に共有されているので最適化の余地がある。置換された内積は、一つの面に対して一つのみで事が足りる。

結び

悲しいことに、そろそろさよならを言わなくてはならない。このシリーズを癇癪を起こすことなく読み切ったら尊敬する。プリュッカー座標系に対して悟りを開いたとしても尊敬する。私が言いたかった事が伝わったなら、すぐに私の家に来て、この雑記に対して何を思ったか教えてくれ。

- Lionel Brits (iam@cadvision.com)

参考文献

[1] http://graphics.lcs.mit.edu/~seth/pubs/pubs.html (訳注:現時点でリンク切れ)
http://graphics.lcs.mit.edu/~seth/pubs/TellerHohmeyerJGT2000.pdf (訳注:現時点でリンク切れ)
[2] http://www.flipcode.com/dp/issue02.shtml
[3] http://www.acm.org/tog/resources/RTNews/html/rtnv10n3.html#art11
[4] http://www.flipcode.com/tutorials/tut_pluecker.shtml
[5] http://www.acm.org/tog/resources/RTNews/html/rtnv11n1.html#art3

このシリーズの他の記事へのリンク

メモ

  • 謝辞は省かせてもらいました。