このブログポストは、Lionel Brits氏のPlücker Coordinates for the Rest of Us - Part 3(2001)を、原著者の許可を得て翻訳・公開したものです。全ての権利は、原著者にあります。

現実世界へ

もちろん、逆の方向へ(訳注:パート2まではデカルト座標系からプリュッカー座標系への変換を話題にしていた)も変換できないといけない。つまりプリュッカー座標と一致する三次元空間での直線があるならばそれを算出できなければならない。プリュッカー座標 $$L={\vec{U_1}:\vec{U_2}}$$ があるとき、 $$\vec{U_2}=\vec{U_1}\times\vec{P}$$ だということは知っている。次の目標は、 $$\vec{P}$$ を見つけだすことだ。

$$\vec{U_2}=\vec{U_1}\times\vec{P}$$ は各要素毎には次のようになっている。

$$\vec{U_{2x}}=\vec{U_{1y}}\vec{P_z}-\vec{P_y}\vec{U_{1z}}$$
$$\vec{U_{2y}}=\vec{U_{1z}}\vec{P_x}-\vec{P_z}\vec{U_{1x}}$$
$$\vec{U_{2z}}=\vec{U_{1x}}\vec{P_y}-\vec{P_x}\vec{U_{1y}}$$

この等式を変換すると、 $$\vec{P}$$ を見つ出すために次の式を解くことになる。

$$ \left[ $$\begin{array}{rrr} 0 & -\vec{U_{1z}} & \vec{U_{1y}} \ \vec{U_{1z}} & 0 & -\vec{U_{1x}} \ -\vec{U_{1y}} & \vec{U_{1x}} & 0 \ \end{array}$$ \right] \left[ $$\begin{array}{rrr} \vec{P_x} \ \vec{P_y} \ \vec{P_z} \ \end{array}$$ \right]

\left[ $$\begin{array}{rrr} \vec{U_{2x}} \ \vec{U_{2y}} \ \vec{U_{2z}} \ \end{array}$$ \right] $$

直線上のどの位置もこの方程式の解として正しいので、解は無限にあることになる(一つに決定することが出来ない)。そのためこの係数の行列は逆行列を持たない。簡約化や何らかの方法でここから進むことができる。このような方程式の一般解は、 $$\vec{P}(t)=\vec{P}+\vec{U_t}$$ のような形をとる。正確な答えについては後で述べる。

次に進む簡単な方法はConorStokes(訳注:flipcodeの関係者のようです)によって指摘された。ベクトル $$\vec{U_2}\times\vec{U_1}$$ は、原点から直線上で最も原点に近いところへ向かうベクトルとなっている。 $$\vec{U_2}=\vec{U_1}\times\vec{P}$$ であることを思い出そう。直線上で最も原点に近い点 $$\vec{P_\perp}$$ について考える。

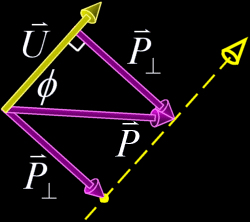
$$\vec{P_\perp}$$ は $$\vec{P}$$ のうち $$\vec{U}$$ に垂直な成分だ。 $$\vec{U}$$ と $$\vec{P}$$ の間の角度で最小のものを $$\phi$$ とすると、 $$\vec{P_\perp}=\vec{P}\sin\phi$$ となる。外積の定義より $$\vec{U_2}=\vec{U_1}\times\vec{P_\perp}$$ だと言えるようになった。次は $$\vec{U_2}\times\vec{U_1}$$ つまり $$(\vec{U_1}\times\vec{P_\perp})\times\vec{U_1}$$ について考えよう。 もうひとつの外積の特徴から次のことがわかる。

$$ (\vec{U_1}\times\vec{P_\perp})\times\vec{U_1}

(\vec{U_1}\cdot\vec{U_1})\vec{P_\perp}- (\vec{U_1}\cdot\vec{P_\perp})\vec{U_1} $$

$$\vec{P_\perp}$$ は $$\vec{U_1}$$ に垂直なので、次のことがわかる。

$$\vec{U_2}\times\vec{U_1} = (\vec{U_1}\cdot\vec{U_1})\vec{P_\perp}$$

すばらしい！ $$L={\vec{U_1}:\vec{U_2}}$$ を $$\vec{U_1}$$ と $$\vec{P_\perp}=\cfrac{\vec{U_2}\times\vec{U_1}}{\vec{U1}\cdot\vec{U_1}}$$ で表現できるようになった。

他の表現方法

ここまで、直線のプリュッカー表現を六次元座標として取り扱った。 $$L_U={\vec{U_1}:\vec{U_2}}$$ のうち、 $$\vec{U_1}$$ は直線の方向を、 $$\vec{U_2}$$ は原点を中心としたトルクやモーメントのアナロジーのようなものになっている。プリュッカー座標の構成要素を互いに独立して扱うこともできる。軸の選択に関して何も制約を課されていないので、構成要素を任意に割り当てることができるのだ。 $$L_U={\vec{U_1}:\vec{U_2}}$$ は、 $$\Pi_{U}=(\pi_{U0},\pi_{U1},\pi_{U2},\pi_{U3},\pi_{U4},\pi_{U5})$$ と等価だ。次のような割り振りが通常は使われる。

$$\pi_{U0}=U_{2Z}$$
$$\pi_{U1}=-U_{2Y}$$
$$\pi_{U2}=U_{1X}$$
$$\pi_{U3}=U_{2X}$$
$$\pi_{U4}=U_{1Z}$$
$$\pi_{U5}=-U_{1Y}$$

または $$\vec{P}$$ から $$\vec{S}$$ への直線から

$$\pi_{U0}=S_{X}P_{Y}-P_{X}S_{Y}$$
$$\pi_{U1}=S_{X}P_{Z}-P_{X}S_{Z}$$
$$\pi_{U2}=S_{X}-P_{X}$$
$$\pi_{U3}=S_{Y}P_{Z}-P_{Y}S_{Z}$$
$$\pi_{U4}=S_{Z}-P_{Z}$$
$$\pi_{U5}=P_{Y}-S_{Y}$$

前のパートでの置換された内積をこれらの表現を用いると次のようになる。

$$\omega = \Pi_U\odot\Pi_V =(\pi_{U0}\pi_{V4}+\pi_{U1}\pi_{V5}+\pi_{U2}\pi_{V3}+\pi_{U3}\pi_{V2}+\pi_{U4}\pi_{V0}+\pi_{U5}\pi_{V1})$$

このプリュッカー座標表現は、三次元でこの直線に交差する全ての直線を含んだ超平面と一致する。良く知られている意味での平面ではなく超平面だ。この超平面はプリュッカー空間を二つに分断する(この超平面で分断された空間は直線の相対方向がそれぞれ時計回りと反時計周りになっている)。この積は $$U(t)$$ と $$V(t)$$ が交差するか、平行か反対方向に平行かのときは0であり、そうでないときは0にはならないという性質を持つ。

何にこれは使えるの？

いろんなことに！さぁ何に使えるか見ていこう。

このシリーズの他の記事へのリンク

• 一般人のためのプリュッカー座標系 パート1
• 一般人のためのプリュッカー座標系 パート2
• 一般人のためのプリュッカー座標系 パート3
• 一般人のためのプリュッカー座標系 パート4 応用編