一般人のためのプリュッカー座標系 パート1
このブログポストは、Lionel Brits氏のPlücker Coordinates for the Rest of Us - Part 1(2001)を、原著者の許可を得て翻訳・公開したものです。全ての権利は、原著者にあります。
はじめに
私が初めてプリュッカー座標系について扱った記事を見たとき、解釈が難しい数学的な幾何表現だなと感じたし、その考え方には馴染めなかった。プリュッカー座標系に関して、簡単に説明してくれる資料が見つからなかったので、構想を含めて一年以上をかけて自分でそれをより親しみやすい形にした。それから最初の記事を改めて見たが、まだまだ大層な言葉と見慣れない表記にあふれていた。それらの記事をお手本にしながら、直線のなす相対的な向きを記述する数学的な方法であるプリュッカー座標系について自分で解釈をしなおした。数時間かけて紙に走り書きを書いたのちに、ついに他の記事で見たようなものを怪しげながらも表現できた。さらに数時間走り書きをした。そして、うぬぼれな心が勝ってしまいウェブというホワイトノイズ上に自分自身の記事を出すことにした。驚くなかれ、まさにその記事をあなたは今読んでいるのだ。幸運を祈る。
慣例的に使われる言葉
一貫性のために、右手座標系をこれからの議論通して使う。
合理的一貫性を持たせるために表記法も他の資料で使われるものを可能な限り使っている。
三次元空間での線の定義
$$R^3$$における直線を定義するには原点$$\vec{P}$$と方向$$\vec{U}$$が必要だ。
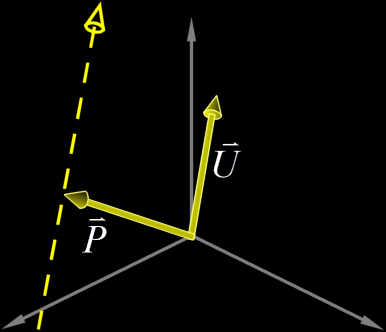
線を定義するのに必要なのは、その原点と方向だけだ。線上のどの位置も、$$\vec{P}$$と$$\vec{U}$$の線形結合で表現できる。単純にこの$$\vec{P}(t)$$の軌跡は、$$\vec{P}$$を通り方向$$\vec{U}$$を向くものとして、tをパラメーターにして$$\vec{P}(t)=\vec{P}+\vec{U}t$$と表現される。
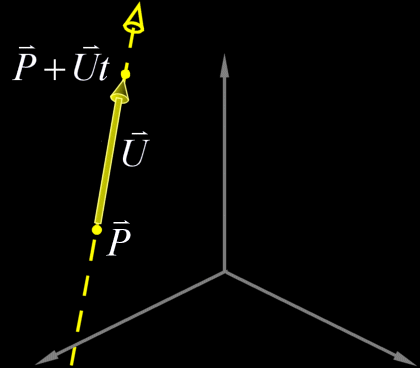
相対的な方向
次に必要なものは、二つの直線の相対的な向き関係を決める方法だ。電磁気学では、ビオ・サバールの法則を使って直線の方向を表現する便利な方法を教えてくれる。この法則は電流$$i$$が電線の中を$$\vec{s}$$に向かっているとき、位置$$\vec{r}$$での磁場$$\vec{B}$$の力と方向を示す。
$$d\vec{B}=\frac{\mu_0}{4\pi}i \frac{d\vec{s} \times \vec{r}}{r^3}$$
我々がやりたいことからすると、この公式はとてもいかめしい見た目なので、本質的なものを抽出する。良く知られている右手の法則は、場$$\vec{B}$$の方向を見つける直感的な方法だ。電線に沿って右手を置き、指は電線を握るよう形にし、親指は流れの方向$$\vec{s}$$に伸ばすようにすることを想像しよう。これで、握った指は$$\vec{B}$$の方向を向いていることになる。

おなじように、直線の「周り」の方向を決めることができる。ある直線の方向を向いたときに、他の直線は時計周りか、反時計回りか、横切るか、平行となっている。次の例では、Line2とLine3はLine1の周りを時計回りに回っていることになる。
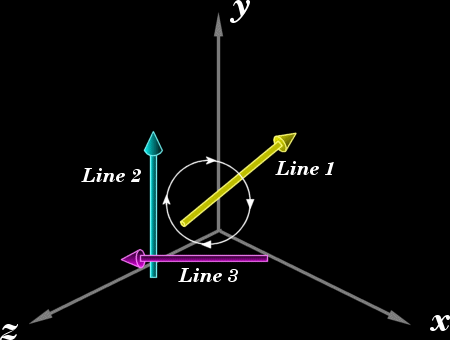
これは電線の周りの磁場$$\vec{B}$$の方向と似ている。物理的な解釈に何ら興味がないので、(ビオ・サバールの法則の)$$\vec{B}$$の方向だけに注目する。同じように考える事で、直線$$\vec{P}(t)$$の周りの場$$\vec{F}$$を定義しよう。簡単のため、$$\vec{P}(t)$$は原点を通過することとする。相対的な方向に関しては、$$\vec{P}$$だけ平行移動しても、$$\vec{P}(t)$$に関する情報は失われない。位置$$\vec{Q}$$での$$\vec{F}$$のベクトル値は$$\vec{U}$$と$$\vec{Q}$$の外積により求められる。
$$\vec{F} = \vec{U} \times \vec{Q} $$
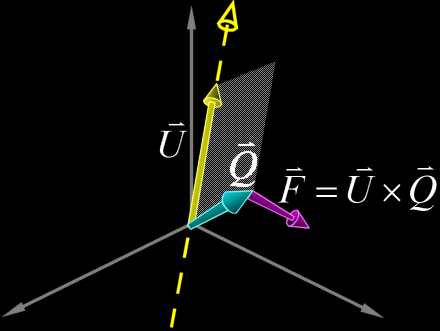
これで、$$\vec{P}(t)$$から見た相対的な方向を判別する強力な方法が手に入った。$$\vec{Q}$$を通り、$$\vec{V}$$を向く直線$$\vec{Q}(t)$$について考える。$$\vec{V}$$と$$\vec{F}$$と同じ方向に向いているなら、この直線は時計周りの方向を向いているだろう。反対に$$\vec{V}$$が$$\vec{F}$$と反対の方向を向いているなら、この直線は反時計周りの方向を向いているだろう。
|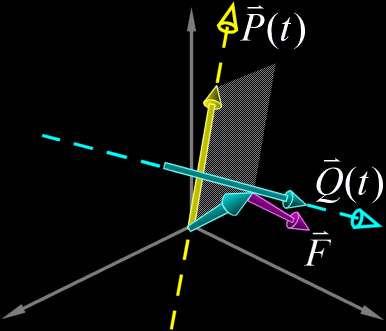 |
|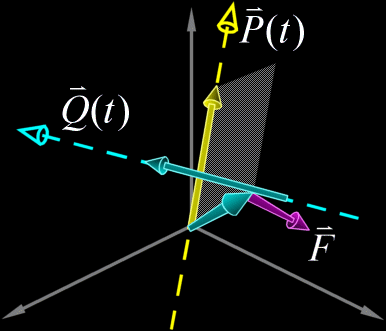 |
|$$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して時計回り|$$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して反時計回り|
|
|$$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して時計回り|$$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して反時計回り|
これらの全ての状態を$$\vec{F}$$と$$\vec{V}$$の内積で表現することができる。ここでは、奥に向かう方向を$$\bigotimes$$で、向かってくる方向を$$\bigodot$$で記述する。(これはダーツの矢が奥に向かうとき、向かってくるときと同じ見え方だ)
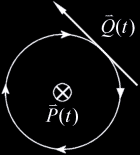
|場合分け 1: | $$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して時計回り|
|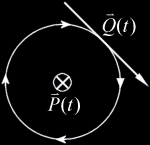 | $$\vec{F}\cdot\vec{V}>0$$ |
|場合分け 2: | $$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して反時計回り|
|
| $$\vec{F}\cdot\vec{V}>0$$ |
|場合分け 2: | $$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して反時計回り|
| | $$\vec{F}\cdot\vec{V}<0$$ |
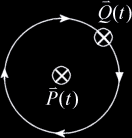
|場合分け 3: | $$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して平行|
|
| $$\vec{F}\cdot\vec{V}<0$$ |
|場合分け 3: | $$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して平行|
| | $$\vec{F}\cdot\vec{V}=0$$ |
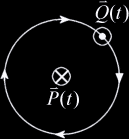
|場合分け 4: | $$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して逆向きの平行|
|
| $$\vec{F}\cdot\vec{V}=0$$ |
|場合分け 4: | $$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して逆向きの平行|
| | $$\vec{F}\cdot\vec{V}=0$$ |
| $$\vec{F}\cdot\vec{V}=0$$ |
補足
$$\vec{F}\cdot\vec{V}=0$$の時にあいまいな点が残っている。$$\vec{Q}(t)$$と$$\vec{P}(t)$$が平行か反対の方向に平行か(それぞれ0度か180度の位置関係だ)、もしくは$$\vec{Q}(t)$$の通過する点$$\vec{F}$$が原点の場合だ。この場合、直線は平行でも逆向きの平行でもない。
$$\vec{P}(t)$$が原点を通っていなくても良いように、$$\vec{P}(t)$$を一般化するべきだ。ふりかえってみよう。二つの直線、$$\vec{P}(t) = \vec{P}+\vec{U}t$$と$$\vec{Q}(t) = \vec{Q}+\vec{V}t$$がある。
位置$$\vec{Q}$$での$$\vec{F}$$は$$\vec{F}=\vec{U}\times(\vec{Q}-\vec{P})$$のように与えられる。
これは次の式と等しい。
$$ \vec{F} = \vec{U} \times \vec{Q} - \vec{U} \times \vec{P} $$
知りたい向きの事を、$$ w $$と呼び、次のように表現する。
$$ w = \vec{F} \cdot \vec{V} = \Bigl[ \vec{U} \times (\vec{Q} - \vec{P}) \Bigr] \cdot \vec{V} $$
これは次の式と等しい。
$$ w=(\vec{U}\times\vec{Q})\cdot\vec{V}-(\vec{U}\times\vec{P})\cdot\vec{V} $$
これは$$ R^3 $$における直線の相対的な方向を表すに十分な表現力がある。
まとめよう。
二つの直線、$$\vec{P}(t) = \vec{P}+\vec{U}t$$と$$\vec{Q}(t) = \vec{Q}+\vec{V}t$$を与えられたら、 $$\vec{Q}(t)$$の向き$$ w $$を$$\vec{P}(t)$$を用いて次のように表現できる。
$$ w=(\vec{U}\times\vec{Q})\cdot\vec{V}-(\vec{U}\times\vec{P})\cdot\vec{V} $$
もし$$ w > 0 $$なら、$$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して時計回りになっている。
もし$$ w < 0 $$なら、$$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して反時計回りになっている。
もし$$ w = 0 $$なら、$$\vec{Q}(t)$$は$$\vec{P}(t)$$に対して平行か、逆向きの平行か、交差している。
時計!手の向き!直線!ああもう!
まだこの話題は終わらない。ここまで話題について来れたなら、次のパートに行ってみよう。
このシリーズの他の記事へのリンク
- 一般人のためのプリュッカー座標系 パート1
- 一般人のためのプリュッカー座標系 パート2
- 一般人のためのプリュッカー座標系 パート3
- 一般人のためのプリュッカー座標系 パート4 応用編