このブログポストは、Brano Kemen氏のMaximizing Depth Buffer Range and Precision(2012)を、原著者の許可を得て翻訳・公開したものです。全ての権利は、原著者にあります。

3Dグラフィックスハードウェアの深度バッファの仕組みはやろうとしている事に対して今日であってもひどく不十分だ。比較的限られた深度のレンジしかないシーンでも、いとも簡単にZファイティングと呼ばれるアーティファクトが発生する。深度バッファの値の利用も恐ろしい。基本的に使える分解能の半分は、ニアプレーンからの二倍のごく短い距離の中で浪費されてしまう。このためニアプレーンをできるだけ遠くに移動させる必要がある。そもそもその行為自体望まれないことだが、さらに悪いことに細かい精度を持つレンジを少し広げようとするだけですぐにまた不十分になってしまう。開発者が知りえる限りの様々なトリックを駆使しても大規模なシーンのレンダリングにはもちろん全く使い物にならない。

この記事は、すぐ目の前に草原がある一方で数百キロ離れたオブジェクトもあるようなシーンも扱える深度バッファの作り方についてのものだ。大半のことはOpenGLを想定して書かれているが、ほとんどのことはDirectXでもできるはずだ。

普通の深度バッファはどのように動いているか

まずは、あまり自明ではないが深度バッファの性質の理解するためには重要な深度の処理の詳細について見ていこう。

普通のパースペクティブな深度バッファはニアとファーのクリッピング面の距離から算出される一般的なプロジェクション行列を使って書かれる。望むようなプロジェクション行列を作れる一方で、パースペクティブ的に正しい深度バッファは特定の条件をその行列が満たしている場合のみ作ることができる。

通常のOpenGLでのパースペクティブなプロジェクション行列では、WとZの値は次のように頂点シェーダーによて計算され出力される。

$$w_p = -z$$
$$z_p = z*(n+f)/(n-f) + 2fn/(n-f)$$

wはカメラプレーンからの正の深度を保持しているということだ。一方でzは一次方程式として表すことが出来る。

$$z_p = -az + b$$

もしくは

$$z_p = aw_p + b$$

頂点シェーダーからの出力値は、Wで割ることで正規化されたデバイス座標系(NDC:normalized device coordinates)になる。そのためZは次のようになる

$$z_{ndc} = a + b/w_p = a - b/z$$

これによって-1から1のレンジにクリップされる。DirectXは0から1のレンジをzに使っているが、基本は同じだ。

仕様によると、頂点シェーダーの出力するパースペクティブ上での補間は、パースペクティブに補間される。 (p/wと1/wにより線形に補間され、それら二つに割られたものはパースペクティブコレクトな値になる) しかし、Zの値だけは線形に補間される。なぜそうするのか？

描画用APIがプロジェクション行列が1/zの項(前に語られたa-b/zのことだ)を持つことを期待するからだ。それをパースペクティブコレクトな方法で補間するには、ハードウェアは線形補間をする必要がある。

さて問題は、深度の比較にもこの値が使われることだ。初めて見たときは深度として使うのにとてもうまくいく関数だと思うだろう。近くのオブジェクトにより高い分解能が割り当てられ、離れれば離れるほど、パースペクティブ中ではより小さくなるため必要な分解能も下がる。しかし現実にはこの関数は近くの位置を表現するのにあまりにもレンジを使いすぎてしまうため、ひどく扱いづらい。レンジの半分は、ニアプレーンから始まり、視点からニアプレーンまでの距離の二倍の間に使いきってしまう。

深度要素に関してパースペクティブ補間ができるならば(noperspective指定が使われない限り既に他の補間では行われている)深度バッファの精度を補間によるアーティファクトを起こすことなく劇的に上げるいくつかの良い方法がある。しかし残念なことにハードウェア機能としてはそのような可能性には注意は払っていないようだ。使えるリソースの範囲で、できることを見ていこう。まずは理想的にはどうあるべきかを。

最適な深度分解能の形

Zファイティングのアーティファクトを避けるために、スクリーン上で同じサイズに見えるカメラからの距離の違うオブジェクト間でもレンジ内なら同じ深度バッファの分解能にならなければいけない。スクリーンに投影されたサイズはジオメトリの深度と逆数の関係で1/zとなる。別の言い方をすれば導関数が1/zに比例するような関数を探すということだ。この関数は対数になる。

理想的な深度バッファを、普通の深度バッファと見比べてみよう。次のグラフ同じパイプラインの32bit浮動小数、24bit対数深度バッファ、32bit対数深度バッファの精度を計算し比較したものだ。

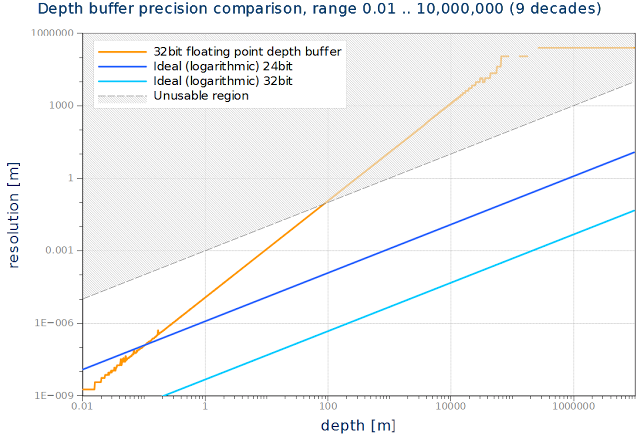
対数分布は9桁の違いを容易に扱うことができ、普通の深度バッファでは、たった4桁のレンジしか使うことができない。4桁というのが普通の深度バッファで得られるレンジだ。“unusable region"に入ると、もはや深度バッファは深度値を適切に解決するできなくなってしまう。一方対数バッファでは、とても余裕がある。実際、グラフにあるよりも少ない16ビットの対数深度バッファでこのシーンを扱うことができる。グラフの軸は、対数スケールであることに注意されよ。

理想的な深度バッファの使い方については、深度バッファの分解能の下限も追加したい。実際に人間の目もあまりにも近すぎるオブジェクトに焦点をあわせることはできないように、目の前、数マイクロメートル先にあるとても小さいオブジェクトのための分解能は必要ない。この対応を入れることで全体の分解能が上がる。詳しくは後で書く。

浮動小数深度バッファ

深度比較に使われる値が深度値そのものだったなら、深度バッファテクニックには浮動小数値は別に問題がない。視点に近ければ値は0に近くなり、浮動小数の精度は上がる。一方視点から遠くなれば必要な深度分解能は小さくなる。オブジェクトまでの距離が離れるに従い1/zに比例してスクリーン上のサイズが小さくなるからだ。

残念なことに、深度比較に使われる値はそれ自体が1/zの関数なので、早々に多くの精度を使い果たしてしまう。

深度バッファで浮動小数を直接使ってもあまりよくない。0に近いほどダイナミックレンジが割り当てられるので、深度バッファは大半のレンジをこの領域で使ってしまい使用に耐えられない。

これに対処するトリックがある。nearとfarを入れ替え、近場のためのレンジを離れた位置のレンジに転用するのだ。これは実際とても効果的だ。1/zの関数形による分解能の減少を、浮動小数の0に近いところの高い分解能がうまく補う。

下のグラフはDirectXにてnearとfarを逆にした浮動小数バッファの分解能を示している。

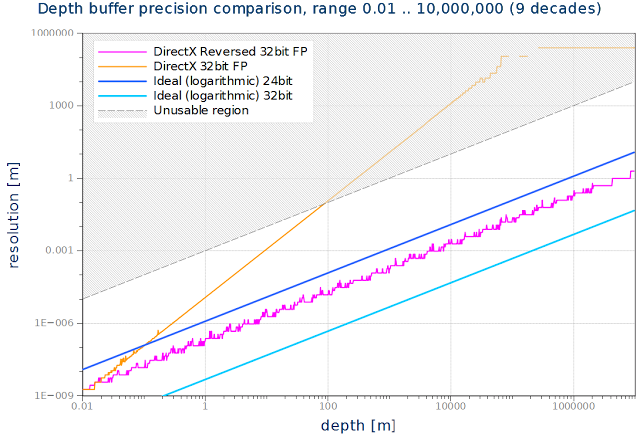
逆にした32ビット浮動小数点バッファは、9桁すべてを通して一貫して24ビットの対数バッファ(32bitの対数バッファは20倍分解能がよくなる)よりもわずかに分解能が優っている。これは素晴らしいことだ。欠点は、24ビットの整数バッファと比べて、8ビット余計に消費することだ。その分でステンシルを使えるかもしれない。

古いハードウェアでは、ビット幅は32ビットにパディングされるためステンシルの利用はフレームバッファーと比べてメモリーを二倍消費し、そのうえより高い帯域もまた要求される。しかしながら今現在ではこれは問題にならない。ステンシルは分離され、深度バッファは最適化されパック化されている。唯一気をつけるとすれば間違えやすいOpenGLのenumに気をかけるくらいだ。

ここまでで、DirectXについてのみ書いていると気がついたかもしれない。そう、このトリックをOpenGLで試しても何も改善しないのだ。

DirectX 対 OpenGL

DirectXよりもOpenGLのファンなので、DirectXよりもOpenGLを使いたい。OpenGLには克服しなければならないことがある。

昔あるとき、ある人が、OpenGLの正規化デバイス座標系はZ軸を含めて-1から1のレンジに全ての軸に対して収まるべきであるとした。 普通は、NDCはカメラを+Zか-Zに投影して中央に配置する。Z軸はスクリーン中央に置かれるので、単に論理的に決めたとしてもXとYは対称になるのだ。じゃあZは？

スクリーン深度軸に対して、カメラ(もしくはニアプレーン)からファープレーンに向かって、0から1のレンジを使う正規化座標系だと思うのは自然だ。深度バッファへも0から1の間にに書かれるならなおさらだ。しかしながら、対称的な世界を願い、どのような理屈よりも対称性がより重要だと決めつけたりして、Zを-1から1のレンジに入れる。もちろん、追加の計算を行い深度バッファへ再投影する必要がある。

$$ 0.5* zc + 0.5 $$

これをどうやって深度バッファの精度問題に結び付けるかって？まず、深度のレンジをさかさまにすることは特に意味がない。なぜなら、ニアプレーンとファープレーンの-1と1を単に逆にするだけだからだ。逆にしても精度がよくなる0付近はニアプレーンの二倍の位置から変わらない。ファープレーンを0に対応させることで結果がよくなるかもしれない。

普通は、OpenGLのプロジェクション行列の3行目は次のようになっている。

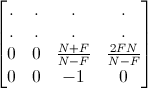
ニアプレーンを-1に、ファープレーンを1に対応している。これを次のようにする。

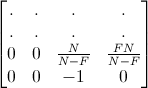
これはファープレーンを0に対応させている。これは本質的にさかさまにした深度のDirectXのプロジェクション行列を正負逆にしたものだ。そのため深度関数は変わらない。(しかし1から0への対応に簡単に変更できる)

1.0でクリッピングが依然として適用されるので、0でクリッピングされるようにしなくてはいけない。しかしこれもまた無視できる場合もある。例えば、Outerra(訳注:原文のブログ上で開発報告がされているゲーム名)では実際にファープレーンより先のジオメトリをクリップする必要がない。どれだけでも遠くに置けるようにしている。

この新しいプロジェクションを使うだけでは問題は解決しない。分解能は依然として悲惨なままだ。問題の二つ目は、再マッピング(0.5zc+0.5)の付加的な項0.5だ。バイアス値0.5は浮動小数の指数部を固定し、0に近い値がもたらす追加の精度を全てを破壊する。これで24ビットの仮数部だけで都合の悪い1/zの形を扱わなければならない。ああ、対称性め！

運がいいことに、NVidiaのハードであればこのバイアス値をglDepthRangeNVを-1から1のレンジを指定して呼び出しでマッピング関数を設定することで間接的に取り除くことができる。これはDirectX形式のマッピングを効果的に設定する。次のグラフはバイアス値のない浮動小数深度バッファの最終的な分解能のグラフだ。OpenGLではファープレーンは0にマッピングされる。分解能は460GTXにて実際に計測されたものだ。

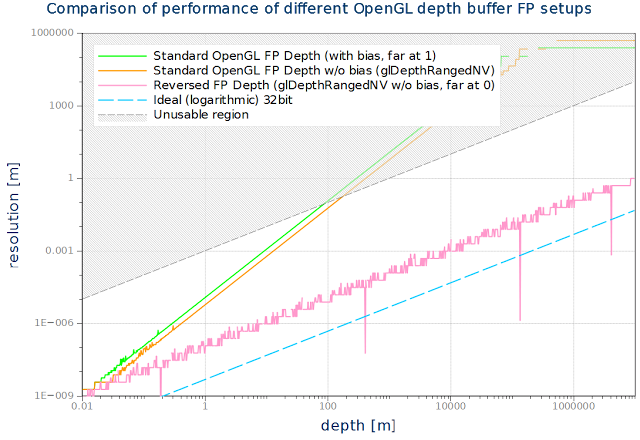
残念なことに、AMDのハードもIntelのハードもNV_depth_buffer_float拡張を使うことができない。ハードウェアの制約で、任意の深度値を出力できない。しかし任意の深度値である必要はない。DirectX形式のバイアス値のない深度マッピングをサポートさえすればいいのだ。OpenGL形式のマッピングを完全に切れるようにするべきだと私は思う。 アップデート: glDepthRangeNVは"AMD Catalyst 13.11 betav9.2 driver"から触れるようになった。

次の点も注意したい。OpenGL 4.2以降の仕様で浮動小数深度バッファ用途ではglDepthRange関数の引数は0から1のレンジにクランプされるという注意書きが削除されたことだ。実装は依然として値をクランプするのを許しているが、事実上仕様を使いづらい何かに変更しようとしている。値はNvidiaのハード上であればクランプされているのだが、仕様に従うためにglDepthRangedNV拡張を使わないといけない。

対数深度バッファ

これまで書いてきたOpenGLのバイアスのない浮動小数深度バッファには二つの問題がある。一つ目はどこでも使えるものではないこと。二つ目はステンシルを使うときに必要なメモリと帯域の増えてしまうことだ。

これまで述べてきた理想的な対数分布を全ての今時のハードウェア上で実際に使える。一つ目はouterraのブログにて書いた。対数バッファの記事を見てくれ。Thatcher Ulrichはのちに少し異なったバージョンを思いついた。

対数深度バッファテクニックは理想的な対数値を頂点シェーダーから出力することで動作する。今は必要ない暗黙のパースペクティブによる割り算を取り除くために、wに事前に乗算する。実装は極めて簡単だ。頂点シェーダーのプロジェクション行列との乗算の後に次のコードを埋め込むだけだ。

{% highlight c++ %} gl_Position.z = 2.0log(gl_Position.wC + 1)/log(far*C + 1) - 1; gl_Position.z = gl_Position.w; {% endhighlight %} もしくは {% highlight c++ %} gl_Position.z = 2.0log(gl_Position.w/near)/log(far/near) - 1; gl_Position.z *= gl_Position.w; {% endhighlight %}

後者はUlrichの方法の変形で、ニアからファーの間全体で相対的な精度が一定という素晴らしい特徴がある。しかし、後で見るように素晴らしいこと(対称であるとか)は常に最善な選択ではない。

明らかに定数項( それぞれ 2.0/log(far*C+1) と 2.0/log(far/near) )は定数値やユニフォーム変数に変更することで最適化をかけられる。また変数"C"はニアプレーンへの距離が0に設定されるので使わない。

このアルゴリズムはとてもうまくいく。全レンジを通して素晴らしい精度を余裕を持って保ってくれる。しかし、カメラに近いところにとても長いポリゴンがあるとうまくいかない。

頂点シェーダーは頂点位置では正確な値を計算できるが、ピクセル上で補間された値は期待された値からずれてしまうからだ。これは次の二つの原因がある。二つの深度値の間の対数関数の非線形性と、ラスタライザでの深度値の暗に線形(つまりパースペクティブではない)な補間だ。フラグメントシェーダー上でgl_FragDepthに対して正確な値を書くことでこの問題に対処できる。

この方法がうまく動作する一方で、たくさんの欠点も抱えてしまう。例えばgl_FragDepthを使うことによる消費帯域の上昇や、深度値に関係する最適化を行えなくするなどだ。これらの問題はある程度対処できるし、その結果は状況による。

フラグメントシェーダーの計算量を減らす

正確なピクセル単位の対数深度を計算するために、深度を補間して、対数を取ることをフラグメントシェーダーでやらないとけない。対数計算はGPU上ではそれなりの速度で行えそうだが、トリックを使ってそれを取り除くことができる。

とても近くにあるオブジェクトで、深度の補間の問題の多くが起こる。オブジェクトのジオメトリーは、ある程度の距離があって初めて十分にポリゴン化されている。接近した三角形はスクリーン上のとても大きな面積を取り、補間された値は正確な値から乖離してしまう。対数カーブを、カメラに近いところだけ線形にすることもできる。つまりフラグメントシェーダーで何の変換も行わずに直接出力するのだ。

等式中のパラメーターCはこの線形化に利用できることがわかる。次のグラフはN/Fの対数関数で、Cを1としたものだ。N/Fはニアプレーンに近付くと精度が高くなる。しかしその場所で精度が欲しかったわけではない。人間の目は非常に近い領域には焦点を合わせることができない。サブマイクロメーター単位の分解能は必要ないのだ。

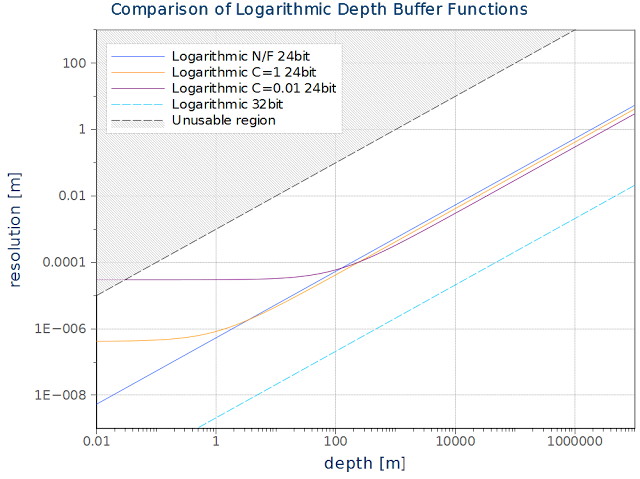
係数Cを補正することで、グラフの平坦な場所の広さを変えることができる(その場所は深度マッピングをする関数の線形になっている場所に対応する)。その平坦な場所の広さをシーンとオブジェクトのポリゴン数に対してちょうどいいところを見つける。C=1であれば線形な場所は拡大したときのエラーを隠しきれなくなるが、C=0.01であればその長さは10メートルになるのでFPSのような視点であれば大丈夫だ。これを使うために、頂点シェーダーにて新しい出力アトリビュートを加えなければならない。

{% highlight c++ %} out float logz; {% endhighlight %}

プロジェクション変換をかけたあとのコードも次のように変更する。

{% highlight c++ %} const float FC = 1.0/log(farC + 1); //logz = gl_Position.wC + 1; //version with fragment code logz = log(gl_Position.w*C + 1)FC; gl_Position.z = (2logz - 1)*gl_Position.w; {% endhighlight %}

フラグメントシェーダーは入力修飾をもち、それをgl_FragDepthに代入する。

{% highlight c++ %} in float logz; void main() { //gl_FragDepth = log(logz)*CF; gl_FragDepth = logz; … } {% endhighlight %}

もしコメントアウトされたバージョンと比べてパフォーマンスが良くならなければ、パースペクティブ補間を(他の補間と同じように)Zに対して入れるのも面白いかもしれない。それはフラグメントシェーダーで明示的に深度値を書かなくても直接使うことができるのだ。繰り返しになるが、深度比較を直接行うためにハードウェア上で計算することもできるくらいにlog命令は極めて高速だ。とにかく両方ともハードウェアレベルでの変更が必要そうだ。

保守的な深度

gl_FragDepthへ書き込むことは早期Zカリングの最適化を切ってしまう。これが問題になる状況もあり得る。対数関数は単調関数なので、ARB_conservative_depth拡張 を使うことができる。これはフラグメントシェーダーから出力される深度値は常に補間された値よりも後ろ(もしくは前)であるというヒントをドライバーに与えるものだ。こうすることで、フラグメントが破棄されるときにシェーダーの評価がスキップされる。

“保守的な深度"を使うにはgl_FragDepthをフラグメントシェーダー内で再度宣言する必要がある。

{% highlight c++ %} #extension GL_ARB_conservative_depth : enable layout(depth_less) out float gl_FragDepth; {% endhighlight %}

最初はdepth_greaterというヒントを与えるのがよいと考えるかもしれない。対数カーブを横切るものはそれの上にあると思うだろうから。しかし驚いたことに、適切なヒントはdepth_lessなのだ。なぜならばZ値はラスタライザーで線形に補間されるからだ。 つまりgl_FragDepthに設定する補間はパースペクティブに補間される。p/wや1/wによって線形に補間したあとに、その二つの和で割ることで正確な値を得る。つまり次の二つの違いだ。

{% highlight c++ %} ((1-t)log(A+1) + tlog(B+1)); ((1-t)log(A+1)/A + tlog(B+1)/B)/((1-t)/A + t/B) {% endhighlight %}

次のことがわかる。パースペクティ的に補間された値は線形に補間されたものの後ろに回る。GL_LESSによって比較することは、カメラにより近い値のみがgl_FragDepthに書かれるということだ。残念なことに、それは早期Zカリングには何の役にも立たない。

気休めとしてはOuterraでは、たとえ明らかなジオメトリバグがあっても、このヒントを逆に設定しても何もスピードアップしたことが計測されなかったということだ。

結果比較

Outerraでのパフォーマンス比較を載せる。テレインと草原は、適応的にテセレーションされているため、フラグメントシェーダーにて深度を書き込む必要がない。次の表の"対数(FS)“の列にてのみ、深度をフラグメントシェーダーで書きだしている。フレームレートの低下のほとんどはオブジェクトによって覆われるスクリーン上の面積(とオーバードロー)が原因だ。

フラグメントで深度が書かれる広大なエリアを持つシーン。ステンシルは使われていない。深度バッファのフォーマットはDEPTH32F_S8であるが、NvidiaのDEPTH32Fフォーマットとパフォーマンスは変わらなかった。表ではフレームレートを表示している

| |逆の浮動小数 |対数(VSのみ)|対数(FS)| |Nvidia 460GTX 310.54| 30 | 30 | 27(-10%)| |AMD 7850 12.11 b8 | - | 48 | 44(-8%) |

56.5万のポリゴン(66.0万がシャドウマップのために)、35.6万の面がテレインに使われている。

同じシーンであるが、スクリーン上にオブジェクトは小さく写っている場合。フラグメントでの深度書き込みの帯域消費は少ない。ステンシルは使われていない。表ではフレームレートを表示している。

| |逆の浮動小数 |対数(VSのみ)|対数(FS)| |Nvidia 460GTX 310.54| 32 | 32 | 32 | |AMD 7850 12.11 b8 | - | 48 | 47 |

オブジェクトは32.7万の面、テレインは33.9万の面、草原は数百万の面。

ステンシルを使った水面の描画を伴うシンプルなシーン。深度とステンシル(32ビットの深度と8ビットのステンシル)のための帯域を増やすためにパフォーマンスはこのOuterraでのシーンでは少し低下する。フィルレートがネックになる他のプログラムやシーンでは違いはより大きくなる。表ではフレームレートを表示している。

| |逆の浮動小数 |対数(VSのみ)|対数(FS)| |Nvidia 460GTX 310.54| 57 | 58 | 58 | |AMD 7850 12.11 b8 | 54 | 56 | 56 |

まとめ

深度バッファの表現レンジと精度を上げる方法がいくつかあるが、残念なことにそれら全てはハードウェアやドライバーのサポートが必要だった。OpenGLでは、正規化された深度座標系を深度バッファに再変換するときのOpenGLのパイプラインが使うバイアス値を取り除くために、絶対値を小さくした。今現在は、NVidiaでのみ可能だ。DirectXでも同じモードが使われているため、他のベンダーもこれをサポートする可能性が高い。

もっとも良いと思われる選択肢は、最適な深度バッファの使用方法をハードウェア側でサポートすることだ。そうなれば、深度とステンシルに関して必要な帯域を減らせることになる。16ビットの対数バッファでさえ、広大な規模を完璧な精度で表現できる。24ビットの対数バッファは宇宙規模のものを表現できる。次の最善な選択肢はz要素のパースペクティブな補間だ。パフォーマンスを損なうことなく線形の深度と対数の深度を使えるようになる。

Outerraでは、たくさんの最適化を施した対数深度バッファを使っている。保守的な深度も、線形化も明らかなパフォーマンスの向上をもたらさなかった。十分なポリゴン数のないオブジェクトのときのみそれらを使い、それ以外の場合は使わないように、フラグメント深度を動的に制御することで多くの場合、パフォーマンスは向上した。この閾値をまたぐ動的にテセレーションされるオブジェクトについては興味深いが、まだ試していない。

メモ