分散の逐次更新
分散をサンプルが増える度に逐次更新したい。
教科書的実装
サンプルが $x_1,x_2,..,x_{n-1},x_n$ のn個あったとき、そのサンプルの不偏分散は次のようになる。
$\overline{x_n}$は$x_n$までの相加平均で次のように算出する。
これをコードに落とし込むことを考えたとき、自然に考えると(2)式を実行して相加平均を得てから、(1)式を実行しそれぞれのサンプルの偏差を求める形になる。これは事前に全サンプルが手元にあり、そこから分散を算出する場合は最速の方法かつ後述するどの方法よりも精度が高い。しかしサンプルが手に入る度に分散を算出したくなった時に、そのたびに相加平均と偏差を出し直さなくてはならず、O(n)の計算量が必要になり、nサンプルまでこれを繰り返すと結果的にO(n^2)の計算量が必要になる。もしサンプルが手に入るたびにしなければならない計算量を定数にできれば、全体の計算量をO(n)に出来る。
単純な変形と問題
逐次計算できるように、それまでのサンプル数に依存しない計算量で行えるような方法を考える。(1)式を展開する。
この結果を素直を利用するならば、前回のサンプルの総和と、前回のサンプルの二乗の総和を持っておけば、新しいサンプルが追加されても、新しいサンプルを加えた総和と、新しいサンプルを加えた後の二乗の総和は定数時間で計算できるため、新しい分散も定数時間で求めることができる。一見これで良さそうに見える。しかしサンプル数が増大したときにこの方式は破綻する。不偏分散はサンプル数には寄らない数値(母集団の分散、母分散)に収束するため、サンプル開始時からずっとその真値は変化しない。しかしカッコの中の式の二つの数値はサンプルが増えるたびに増大していく。このような形式のためサンプル数が増えれば増えるほど、不偏分散はその桁落ち誤差に埋もれていく。これは避けなければならない。
Welfordの方法
桁落ち誤差が発生しないような方式を考える。このような方法にWelfordの方法がある。これは平均と不偏分散を変形したものの漸化式を利用するものだ。まずは相加平均の漸化式を見つける。
分散
次に不偏分散の漸化式を出してみるが、そのままではうまくいかない。$s_n^2$を次のような$M_n$で置き換える
この$M_n$の変化量を式変形していくと次のようになる。
& = \sum_{x=1}^{n+1} x_{i}^2
- 2 \overline{x_{n+1}} \sum_{x=1}^{n+1} x_{i}
- (n+1)\overline{x_{n+1}}^2
- \sum_{x=1}^{n}x_{i}^2
- 2 \overline{x_{n}} \sum_{x=1}^{n} x_{i}
- n \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- 2 \overline{x_{n+1}} \sum_{x=1}^{n+1} x_{i}
- (n+1)\overline{x_{n+1}}^2
- 2 \overline{x_{n}} \sum_{x=1}^{n} x_{i}
- n \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- 2 \overline{x_{n+1}} (n+1) \overline{x_{n+1}}
- (n+1)\overline{x_{n+1}}^2
- 2 \overline{x_{n}} n \overline{x_n}
- n \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- 2 (n+1) \overline{x_{n+1}}^2
- (n+1)\overline{x_{n+1}}^2
- 2 n \overline{x_n}^2
- n \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- (n+1) \overline{x_{n+1}}^2
- n \overline{x_n}^2 \nonumber \\
& = x_{n+1}^2
- (n+1)( \overline{x_{n+1}}^2 - \overline{x_{n}}^2 )
- \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- (n+1)( \overline{x_{n+1}} + \overline{x_{n}} )( \overline{x_{n+1}} - \overline{x_{n}} )
- \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- (n+1)( \overline{x_{n+1}} + \overline{x_{n}} ) \frac{1}{n+1} ( x_{n+1} - \overline{x_{n}} )
- \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- ( \overline{x_{n+1}} + \overline{x_{n}} ) ( x_{n+1} - \overline{x_{n}} )
- \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- \overline{x_{n+1}} x_{n+1}
- \overline{x_{n+1}} ~ \overline{ x_{n} }
- \overline{x_{n}} x_{n+1}
- \overline{x_{n}}^2
- \overline{x_{n}}^2 \nonumber \\
& = x_{n+1}^2
- x_{n+1} \overline{x_{n}}
- \overline{x_{n+1}} x_{n+1}
- \overline{x_{n+1}} ~ \overline{ x_{n} } \nonumber \
& = (x_{n+1} - \overline{x_{n+1}}) ( x_{n+1} - \overline{x_n} ) \nonumber \\
\end{align} $
$\overline{x_{n+1}}$と$\overline{x_n}$ は前の漸化式で求まるので、これで $M_n$ の漸化式を得た。不偏分散は $M_n$ を $n-1$ で割れば良いので、これで不偏分散の逐次更新ができるようになった。大抵の場合は$x_{n+1}$,$\overline{x_{n+1}}$,$\overline{x_{n}}$ は同じ程度の数値なので、桁落ち誤差が発生するような計算はなくなり、良い精度が期待できる。実際に単純な変形をした二つ目の方法よりもずっと精度が良く、教科書的な実装にそれなりに近い結果になる。
共分散
共分散も1パスで出せる。共分散の定義は
となり、標本の共分散は
TODO: ここで、nをかけた変数を用意してあげてそこから導出する
となる。n番目の標本までの標本共分散を'$s^{n}$‘としておくとn+1番目の標本共分散’$s^{n+1}$‘は
なので、$s^{n}$と$s^{n+1}$の差は
結果
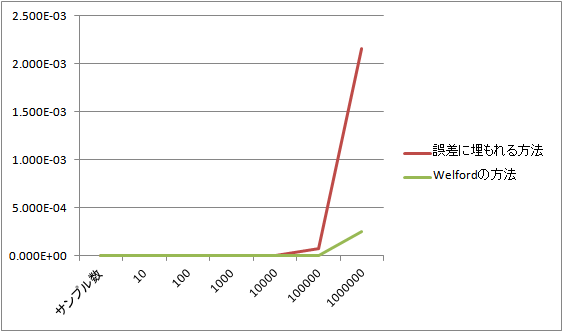
[0,1)の一様乱数に対して、様々なサンプル数で分散を出し、教科書的なベタ実装に対して誤差を出したグラフが以下だ。サンプル数が増えるとWelfordの方法の方がずっと誤差が少ないことがわかる。
その他
- 単純に教科書的な方法を実装すると$\sqrt{n}$に比例した誤差が発生する。補正加算を用いるとより正確な数値を得られる。詳細はWikipediaで。
- サンプルにウェイトがある場合(i.e.レイトレ)にも応用することが出来るWestの方法がある。詳細はWikipediaで。