複利と分散
利率に分散がある複利の結果を解析的に求めたい。
複利の計算は初等教育で習うほど単純な累乗の計算だが、複利に分散が入りこむものも世の中には存在する。このようなものに対して、分散が含まれていない複利の計算から得られる直感はどの程度妥当なのかを確認する。
要約
先に要点をまとめる。分散がある複利は、次のような直感的ではない性質を持つ。
- 分散のある複利で得られる期待値は、分散がないときの複利で得られる期待値と等しい。
- しかし最頻値と中央値は平均値と等しくなく、双方とも平均値を 必ず下回る。
その乖離は、分散が大きくなると共に増える。 - 総リターンの分散は時間と共に発散していく。その速さは複利の分散の大きさに依る。
かみ砕くと次のようになる。
- 価格の波が大きな商品ほど、極一部の「とても儲かった人」と
大部分の「そこまで得をしていない人/損した人」の二極化を拡大させる。
このような結論がなぜ導かれるかについて順を追って説明する。
単純な複利
利子には単利と複利がある。
単利$R$のものを$n$年保有した場合は、元本は$1+nR$倍となる。単利が5%のものを10年保持すれば$1+0.05*10=1.50$となり元本が1.5倍になる。年数に比例して利益が拡大するため直感的だ。
一方複利とは利子のもう一つの形で毎年決められた利率が、元本とそれまでの利子にかかる。複利$R$が$n$年かかった場合、元本は$(1+R)^n$倍となる。複利が5%のものを10年保持すれば$(1+0.05)^{10} = 1.63$となり元本が1.63倍になる。単利と違い利率が低かったとしても文字通り指数的に元本が増加していく。
このように、単純な算数の世界で完結するものものあるが、現実世界には複利に分散があるもの(リスク資産)も存在する。これも同様の考え方で扱ってもいいのだろうか。
分散がある複利
世の中には複利に分散があるもの(リスク資産)もある。例えば日本の年金積立金管理運用独立行政法人(GPIF)は、アセットクラス(リスク資産の分類)毎に利率と分散を予測したものを公開している。期待リターンと書かれているものが予測された利率で、リスクと書かれているものが予測された利率のばらつきの1標準偏差だ。「国内株式」の「期待リターン」と「リスク」と書かれたところを見るとそれぞれ「3.2%」と「25.1%」と書かれているのでこれは「平均利率が3.2%、1標準偏差が25.1%の範囲」ということを意味する。このように、ある種のリスク資産は利率(リターン)とそのばらつきの標準偏差(リスク)が予測値ではあるが求まっている。問題はこれをどのように解釈するかだ。
誤った直感
平均利率(期待リターン)とそのばらつき具合を表す標準偏差(リスク)についての解釈については次のようなものが「直感的」だ。
「長い時間が経てば、ばらつきが相殺されるのだろうから、期待リターンにだけ着目すればいいのだろう」
これはなんとなく信じられる気がするが、実は長期間経過しても、総リターンは期待リターンAには収束しない。
正しいリターンとリスクの定義
リスク資産に関して、期待リターン($\mu$)とリスク($\sigma$)が与えられた場合、これは正確には次のようなことを意味している。
「連続複利が平均$\mu$、分散$\sigma^2$の正規分布に従うように価格が推移する」
ここで出てきた用語について順を追って説明する。
連続複利
複利は「年率5%」といった形でよく表される。これを仮に「内部的には半年に一回の複利計算が2回行われていた」と考ると、その半年毎に計算されていた複利は次のように算出できる。
$$
1.0 + 0.05 = (1.0 + \cfrac{r}{2})^2 \
r = 2((1.0 + 0.05)^{1/2} - 1.0) = 0.0494
$$
この「内部の計算間隔」をさらに細かく「内部的に四半期毎に4回計算されていた」「内部的に月次で12回計算されていた」と考えるとその時の複利は次のようになる。
|頻度 |内部の複利| |年次 |$$0.05000 = 1((1 + 0.05)^{1/1} - 1)$$| |半年次 |$0.04939 = 2((1 + 0.05)^{1/2} - 1)$| |四半期 |$0.04909 = 4((1 + 0.05)^{1/4} - 1)$| |月次 |$0.04889 = 12((1 + 0.05)^{1/12} - 1)$| |週次 |$0.04881 = 52((1 + 0.05)^{1/52} - 1)$| |日次 |$0.04879 = 365((1 + 0.05)^{1/365} - 1)$|
間隔を狭めれば狭めるほど内部の複利は小さくなっていくが、なんらかの定数に漸近しているように見える。 内部的に分割している数を$n$、外部から見える年利つまり実効年率$r_{EFF}$として$n$を無限に持っていった極限を考える。
$
\begin{align}
r_{COM} & = \lim_{n \to \infty} n((1.0+r_{EFF})^{1/n}−1.0) \nonumber \
& = \lim_{m \to 0} \cfrac{(1.0+r_{EFF})^{m}−1.0}{m} \nonumber \
& = \lim_{m \to 0} \cfrac{f(m)−f(0)}{m-0} \nonumber \
& = f'(0) \nonumber \
& = (1+r_{EFF})^{0} ln(1+r_{EFF}) \nonumber \
& = ln(1+r_{EFF}) \nonumber \
\end{align}
$
ここで式の変形には、$m=1/n$の置換、$f(x)=(1+r_{EFF})^x$の導入、微分の定義を使っている。この極限値の事を __連続複利__ (Continuous compounding)と呼ぶ。先の年率5%の例では連続複利は$ln(1+0.05)=0.04879$となる。連続複利から、実効複利への換算は先の式を変形して
$ r_{EFF} = e^{r_{COM}} - 1 $
となる。連続複利の形式に変換しておくと、任意の時間の利率を逆算することができる。例えば321日毎の複利であれば
$ e^{0.04879*\frac{321}{365}} - 1 = 0.04384 $
時間間隔は一年以内である必要がないので、10年間毎の利率、つまり年率5%のものを10年持った場合の複利も直接計算できる。
$ e^{0.04879*10} - 1 = 0.62889 $
これは通常の複利計算の結果$1.05^{10}-1.0=0.62889$と一致する。連続複利の形式になると複利操作が楽になる。例えば一年目の利率が$r_1$、二年目の利率が$r_2$だとすると、二年間での複利は次のように計算していた。
$ R = (1+r_1)(1+r_2) - 1 $
これがもし一年目の連続複利が$r_1$、二年目の連続複利が$r_2$だとすると、二年間での複利は次のようになる。
$
e^{R} = e^{r_1} e^{r_2} \
R = r_1 + r_2
$
最初の二年の複利の連続複利が$r_1$で、次の3年の複利の連続複利が$r_2$であった場合も
$
R = 2r_1 + 3r_2
$
と至極簡単な表現にすることが出来る。つまり連続複利は、複利計算が単純な足し算に置き換えられるということになる。
ここまでの流れをまとめる
- 「期待リターンとリスク」は、普通の複利ではなく、連続複利上で定義されている。
- 複利の計算での乗算除算は、連続複利では加算減算になる。
対数正規分布
正規分布に従う確率分布の加算の結果の分布は、正規分布のパラメーター$\mu$と$\sigma^2$を加算した結果をパラメーターに持つ正規分布に従うことが知られている。これを「再生性を持つ」という。式で表現すると次のようになる。
$
x_1 \sim N(\mu_1, \sigma_1^2) \
x_2 \sim N(\mu_2, \sigma_2^2) \
x_3 = x_1 + x_2 \
x_3 \sim N(\mu_1+\mu_2, \sigma_1^2 + \sigma_2^2)
$
この再生性を利用して、正規分布$N(\mu, \sigma)$に従う連続複利をn年分足し合わせた結果を求める。
$
r_1 \sim N(\mu_1, \sigma_1^2) \
r_2 \sim N(\mu_2, \sigma_2^2) \
… \
r_n \sim N(\mu_n, \sigma_n^2)
$
これらの連続複利の和、つまりn年目での連続複利上での収益率の分布$R_{COM}$は次のようになる。
$
r_{COM} = x_1 + x_2 + … + x_n \
r_{COM} \sim N(\mu_1+\mu_2+…+\mu_n, \sigma_1^2 + \sigma_2^2+…+\sigma_n^2)
$
全ての$\mu_i$と$\sigma^2_i$は等しいので、
$ r_{COM} \sim N(N \mu, N \sigma ) $
となる。この$r_{COM}$から実効利率$r_{EFF}$を出すには前出の式から次のようになる。
$
r_{COM} \sim N(n\mu,n\sigma^2) \
r_{EFF} = e^{r_{COM}} \
r_{COM} = ln(r_{EFF})
$
つまり収益率$r_{EFF}$は、正規分布の$x$を$ln(x)$で置き換えた式になる。$\cfrac{ln(x)}{dx} = \cfrac{1}{x}$であることに注意すれば
$ f(x) = \cfrac{1}{\sqrt{2 \pi \sigma'^2 } x} exp \biggl( { -\cfrac{ (ln(x)-\mu')^2 }{ 2 \sigma'^2 } } \biggr) $
となる。これを対数正規分布$NL(\mu',\sigma'^2)$と呼ぶ。見た目こそ正規分布のようにみえるが、$\mu'$と$\sigma'^2$は正規分布のように平均$E(X)$、分散$V(X)$には相当せず次のような変換が行われる。
$
E(X) = exp(\mu' + \frac{\sigma'^2}{2}) \
V(X) = exp(2\mu' + \sigma'^2) (e^{\sigma'^2} - 1)
$
この$E(X)$,$V(X)$を、$\mu$と$\sigma^2$に置きなおし$\mu'$と$\sigma'^2$について解くと次のようになる。
$
\mu' = ln(1+\mu) - \cfrac{1}{2} ln\biggl(\biggl(\frac{\sigma}{\mu}\biggr)^2 + 1 \biggr) \
\sigma'^2 = ln\biggl(\biggl(\frac{\sigma}{\mu}\biggr)^2 + 1 \biggr)
$
また最頻値は次のようになる。
$ Mo(X) = exp(n\mu' - n\sigma'^2) $
また対数正規分布は正規分布と同じく再生性を持つ。
連続複利が$N(\mu,\sigma^2)$に従う場合、n年後の収益率の確率分布は$\mu'$、$\sigma$を用いて$NL(n\mu',n\sigma'^2)$に従うということがこれで分かった。
実例
実例として先のGPIFの国内株式クラスの予測「期待リターン3.2%とリスク25.1%」に対して、リターンの解析解を出してみる。仮に10年間がずっと同じ数値を維持したと仮定して運用した場合について考えてみる。連続複利が$\mu=0.032$、$\sigma=0.251$に従うので、対数正規分布の$\mu'$と$\sigma'$は次のようになる。
$
\mu = 0.032 \
\sigma = 0.251 \
\mu' = ln(\mu+1) - \cfrac{1}{2} ln\biggl(\biggl(\frac{\sigma}{\mu+1}\biggr)^2 + 1 \biggr) = 0.00276 \
\sigma'^2 = ln\biggl(\frac{1}{n}\biggl(\frac{\sigma}{\mu+1}\biggr)^2 + 1 \biggr) = 0.05747
$
10年分の対数正規分布の$\mu'$と$\sigma'$は次のようになる。
$
n\mu' = 0.02763 \
n\sigma'^2 = 0.57471
$
これから平均値を算出する。
$
E(X) = exp(n\mu' + \frac{n\sigma'^2}{2}) = 1.37024 \
$
また最頻値は次のよう算出される。
$ Mo(X) = exp(n\mu' - n\sigma'^2) = 0.57864 $
平均値は約1.4倍となっているが、残念なことに最頻値では0.6倍弱になってしまい元本割れが発生している。グラフを見てみる。
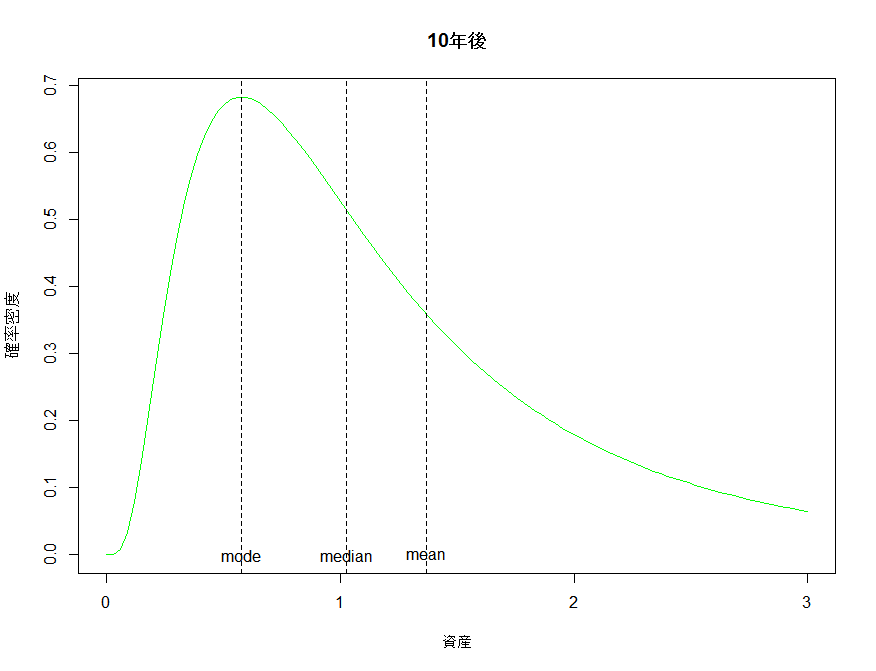
左に大きな山が出来、右に低く長い裾野が出来ている。低く長い裾野が全体の平均値を押し上げているため、平均値は最頻値よりもだいぶ高いところにあることがわかる。これはたまたまこうなったわけではなく、対数正規分布に従う場合は必ずこのようになる。平均値と最頻値の算出式を見比べてみる。
$
E(X) = exp(n\mu' + \frac{n\sigma'^2}{2}) \
Mo(X) = exp(n\mu' - n\sigma'^2)
$
$e$の肩にのっているものの大小関係から常に$Mo(X)<E(X)$が成立するのがわかる。さらに対数正規分布の中央値は次のように算出される。
$ Median(X) = exp(n\mu') $
これらから、$Mo(X)<Median(X)<E(X)$が常に成立することがわかる。分散の時間経過についても考えてみる。n年経過した時点での分布での分散は、前出の式より次のようになる
$
X_n \sim NL(n\mu',n\sigma'^2 ) \
V(X_n) = e^{2n\mu' + n\sigma'^2} (e^{n\sigma'^2} - 1) \
$
となり年々拡大、発散していくことがわかる。一方で面白いことに確率分布は最頻値周辺に時間の経過と共に集中していく。
長期間投資を続けると、最頻値に吸い寄せられていくように見えるのだ。
つまり大多数の人は期待リターンを得る事はできず、一部の幸運な人が期待リターンより遥かに多くを得て、結果平均を押し上げる結果になる。
対数正規分布のCDFはわかるのでそこから最頻値に収束することは確認できます。 {% highlight R %} erfc <- function(x) 2 * pnorm(x * sqrt(2), lower=FALSE) n <- 100 mu <- 1 * n sig <- 1 * n x <- exp(mu-sigsig) result <- 1/2 * erfc(-(log(x)-mu)/(sigsqrt(2)))
[1] 0 {% endhighlight %}
さらに少し寄り道。年換算で最頻値に寄ることを取り上げ「長期間投資すれば、ばらつきが減る」と言われたり、逆に絶対値自体のばらつきが増える事を取り上げ「長期間投資すれば、ばらつきが増える」と言われたりすることがあります。混乱するのですが、全く別の理論が存在するわけではなく、単純に指標が異なるだけです。
この事について少し分かりやすい例えとして、コインを投げる事を考えます。コインは表と裏が各々半分の確率で出ます。
10回投げた時点で、7回表が出て3回裏が出たとします。期待値は当然5回なので、期待とのズレは2回。この期待とのズレを比率で表現することもできます。つまり5回のところを7回だったので7/5 = 1.4と表現します。
表現方法1. 7 - 5 = 2回のズレ
表現方法2. 7/5 = 1.4のズレ
次に1000回投げたとします。510回表が出たとします。投げる回数が増えれば増えるほどより期待値に近い値が出ることはよく知られているので、これは納得感のある結果だと考えられます。先の二つの表現方法では、次のようになります。
表現方法1. 510 - 500 = 10回のズレ
表現方法2. 510/500 = 1.02のズレ
ズレに関して表現方法1を採用すればコインを振れば振るほどズレは拡大していきます。一方表現方法2を採用すれば振れば振るほど期待値に収束していきます。
20年後、30年後の分布のプロット見てみる。
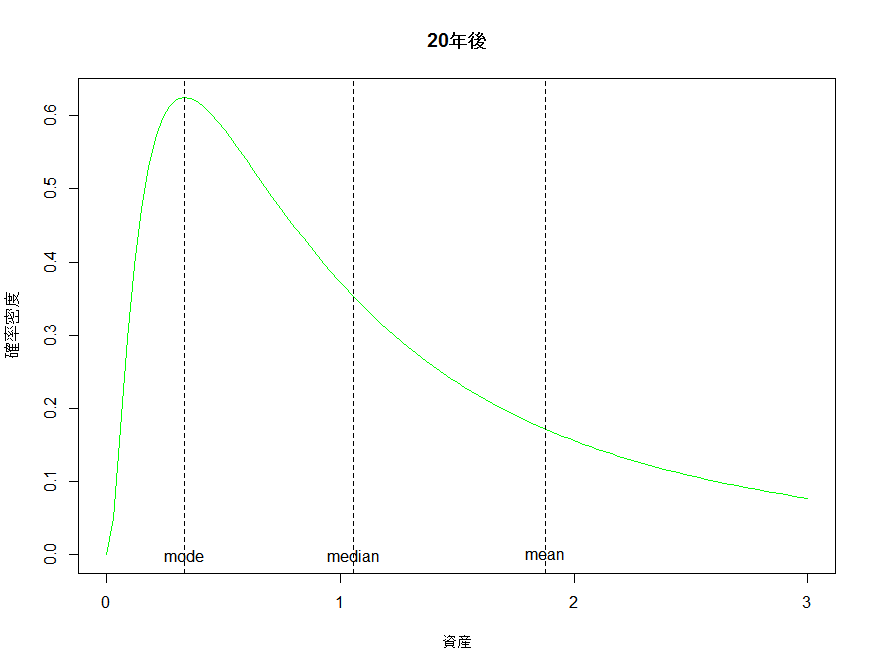
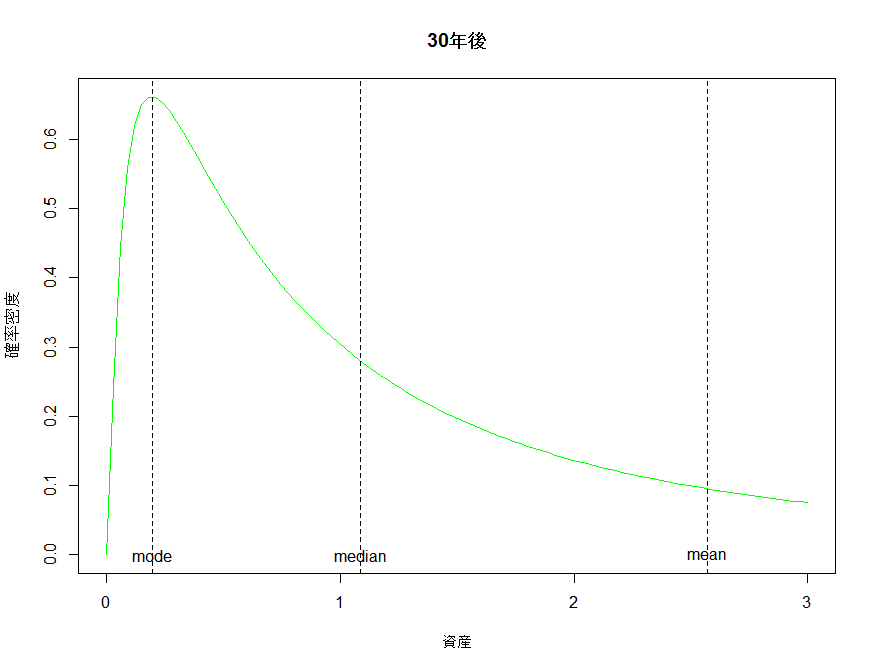
先に書いたように、時間が経つたびに最頻値に全体が吸い寄せられていくのが分かる。
ちなみに、平均値は分散が無い時と同じように動く。72の法則を使って72/3.2≒約23年で元本が二倍になるという皮算用は、平均値に限って言えばしっかりと機能している。しかし最頻値は0.28にまで縮小してしまっている。分散があるにもかかわらず期待リターンのみから皮算用をすることがどれほど意味がないかがわかる。
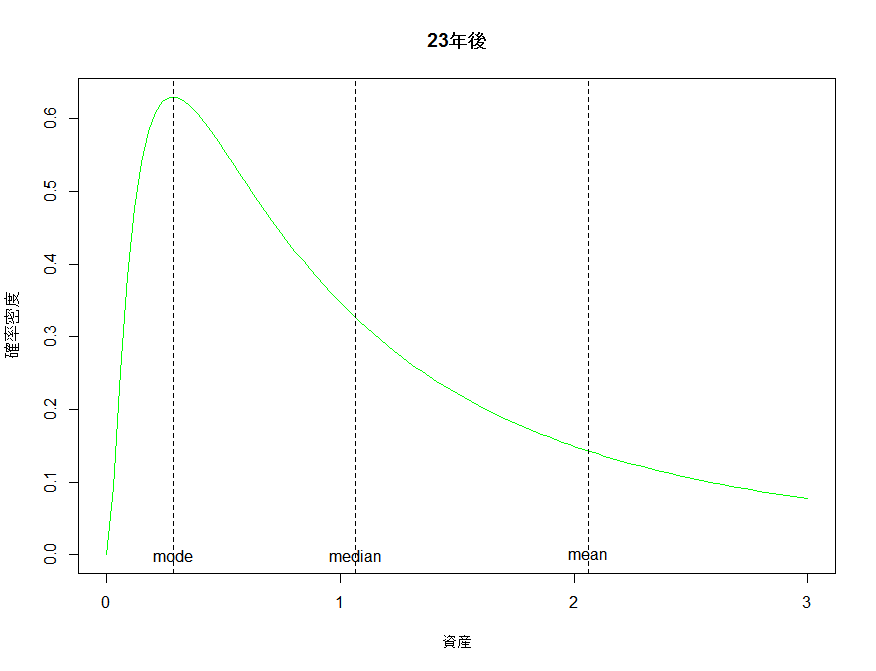
検証コード
{% highlight R %}
定数
mu <- 0.032 s <- 0.251 n <- 30
m <- 1.0 + mu
一年間分の対数正規分布のmuとsdを求める
mud <- log(m)-log((s/m)^2+1)/2 sd <- sqrt(log((s/m)^2+1))
N年分の対数正規分布のmuとsdを求める
mu1 <- mud * n sd1 <- sd * sqrt(n)
通常のmuとsdを求める
mu2 <- exp(mu1+(sd1^2)/2) sd2 <- sqrt(exp((2mu1)+sd1^2)(exp(sd1^2)-1)) mode <- exp(mu1-sd1^2) median <- exp(mu1)
LN(mu1,sd1^2)の分布を描画する
x <- seq(0, 10, 1.0); curve( dlnorm( x, meanlog=mu1, sdlog=sd1 ), from=0, to=3, col=“green”, xaxp=c(0, 10, 10), main=“20年後”,xlab=“資産”,ylab=“確率密度” )
平均値
text(mu2, 0, “mean”) abline(v=mu2, lty=2)
最頻値
text(mode, 0, “mode”) abline(v=mode, lty=2)
中央値
text(median, 0, “median”) abline(v=median, lty=2)
print( paste(“mu “,mu2)) print( paste(“mode “,mode)) print( paste(“median “,median)) print( paste(“sd “,sd2)) {% endhighlight %}
参考
[1] ツヴィ・ボディ, アレックス・ケイン, アラン・J・マーカス, 証券投資(上), 2003
[2] リスク資産の複利確率. http://www.fund-no-umi.com/blog/h/index.html
[3] 梅屋敷商店街のランダム・ウォーカー. http://randomwalker.blog19.fc2.com/
[4] 騰落率がプラスでも資産減 長期投資の落とし穴. http://www.nikkei.com/money/features/76.aspx?g=DGXMZO8364607025022015000000&df=1
雑記
派手な話ほど目立つので当然だとは思うのですが、リスク資産についての話は、「いくらいくら儲かった」のような派手なものが多いです。そのような話を見聞きするたびに、「相場を読める人がいるから」とか、陰謀だとかを勝手に仮定しがちです。しかしそれらを一切仮定せず、単に分散があるということを仮定しただけでも「一部の派手な話の下に屍が沢山ある」状態が作れるということを算数を使って説明できたのでとても満足しています。
入社式の季節です。新入社員が財形貯蓄/確定拠出年金の説明をされる季節でもあります。私自身もそうでしたが、それが初めてリスク資産について触れる機会になる人も多いと思います。その時に、「よくわからないし、天引き貯金として使おう」でもいいですが、せっかくなので私が推す「インデックス(市場の平均値)のバイ&ホールド(買いっぱなし)」について一考して欲しいと思い、その時に必要になる算数の一部について、私の知っている限りの知識でではありますがまとめてみました。より詳しく正確に知りたい方は、敗者のゲーム、ウォール街のランダム・ウォーカー、証券投資、ほったらかし投資術などを参照してください。
※20150524追記: ほったらかし投資術の全面改定版が6月に出るそうです!(URL)
実は上の「分散は相殺される」ことについて、確定拠出年金か何かの説明会でされた覚えがあります。「若年時から積み立てれば、時間があるのである程度のリスクは許容できる」みたいなぼんやりした説明だったと思いますが、これは「分散は相殺される」的なミスリードを誘います。年換算の収益率が最頻値に収束することを指していたとしても、リスクの影響を受ける最頻値を取り上げるのはおかしな話です。今考えたら単に「失敗しても稼ぐ時間はあるから大丈夫でしょ?」位の意味合いだったのでしょう。これは買い手から考えた場合、あまり合理的な感じはしません。当時は全く違和感なく納得していたのですが。
個人的には確率統計の教材としても良いと感じました。ここでは書きませんでしたが、「分散が低い方が良い」という帰結から、類書では分散を下げる試みについて色々書かれています。伝わる人には伝わると思うのですが 「分散を限界まで減らそうとする努力」はこのサイトのメインテーマ(?)であるレイトレのノリそのものです 。結果的に使われる確率統計の知識も相補的となりとても面白く感じます。
期待リターンとリスクについてですが、ズバリ「期待リターンA% リスクB%」と書いてある資料を見ると、あたかもそれが完璧に実現されそうな錯覚に陥りますが、リスクの推定に比べて、平均リターンの推定というものは割と正しく出ないそうです(そもそも算出している団体によりかなりばらつきがある)。じゃあこれまでの計算は全て無駄かと言えばそうでもなくて、「どれ程の速度で目減りするものか」「そもそも最頻値で最終的なリターンはプラスになりえるのか?」というのがおおよそわかるので心の準備ができたり、分散が異常に高い商品に近づく気力が削られるかなと思っています。少なくとも期待リターンのみに着目した安易な狸の皮算用を始めた場合に比べて、いくらか高級な思考ができると思います。
最後に、ここで書いた全てのことは「相場観は全くない、未来予測が全くできない」という前提で書かれています。もし正しい相場観があり、正確に未来予測が出来るならば「安く買って高く売る」ということが容易にできるでしょうから、わざわざ確率分布などは持ち出さなくていいのです。実際にそれに近いことが出来る人がいても不思議じゃないというのが率直なところです。しかしなろうと思っても非常に難しそうですし、仮になれたとしてもその労力が見合うか不明ですし、「読めている」のか「読めている気になっている」かを判定するには検定の知識が必要になり、確率統計を結局使う羽目になりそうなのが面白いです。少なくとも大多数の人がなることは不可能ではないかなと思っています。仮に「全ての人が未来予測が出来る」ならば一切の取引は成立していないはずでしょうから。