区間演算と交差判定

July 22, 2018

この記事はレイトレ合宿6のアドベントカレンダーの4週目の記事です。

はじめに

レイトレーシングは浮動小数点演算の塊です。浮動小数点は実数を表現するためのものではありますが、実際には全ての実数を表現できることができず、表現しているものや、その演算の結果には誤差を伴います。この誤差に注意を払った場合とそうでない場合で、最終画像に大きな違いをもたらすかもしれません。この記事ではPBRT V3でも一部注意が払われることになった浮動小数点演算について触れ、最後に特に交差判定での実例について書いていきます。

浮動小数点

レイトレの文脈で__浮動小数点__とあればほぼ__IEEE 754の単精度浮動小数点__の事を指すのでこれ以降はこれを単精度浮動小数点と呼びます。単精度浮動小数点は、符号部1bit、指数部8bit、仮数部23bitからなる32bitの値で非常に小さい値から、大きい値まで広いダイナミックレンジを表現することができます。

引用: Wikipedia|Single-precision floating-point format

しかし一方で無限の精度があるわけではないので、たまたまぴったり表せる値(1や0.0625など)以外は近似値としてしか表すことが出来ません。またたまたまぴったり表せる値であっても、それらが演算された結果は例外的な場合(1.0+1.0など)を除きそれらも近似値になります。実際にどんな値をぴったり表せるかはIEEE-754 Floating Point Converterで確かめることができます。触ってみると意外と離散的な値であることを実感できます。

お役立ち情報: 想像以上に単精度浮動小数点は離散的
下のテーブルは基準を1とした時に表現できる最小の単位の比較です。

基準 float double

部屋の大きさマイクロメートル陽子の大きさ

地球 2.4m ナノメートル

太陽までの距離 10km 髪の太さ

一日 5m秒ピコ秒

一世紀 3分マイクロ秒

ビッグバンから 1000年数分

基準	float	double
部屋の大きさ	マイクロメートル	陽子の大きさ
地球	2.4m	ナノメートル
太陽までの距離	10km	髪の太さ
一日	5m秒	ピコ秒
一世紀	3分	マイクロ秒
ビッグバンから	1000年	数分

引用: I LIKE BIG BITS|Float or double?

さてこのように離散値しか扱うことができないため、一般的な浮動小数点演算の結果は近似値の近似値の近似値の…近似値になっていたりします。これでは一体何が正しいのかわからなくなりそうですが、一方で単精度浮動小数点には精度に関して満たすべき仕様が決められています。

「浮動小数点の四則演算と平方根の演算の結果は無限精度で演算した場合と比較して0.5ULP以内になっていなければならない」

ULP(Unit in the last place)

実数は無限集合なので、「2.0の隣の数」といったものが存在しません。一方で浮動小数は有限のビットで実数を表現する以上、可算集合となるので__「2.0の隣の数」が存在します__(そしてそれは2.0000002384185791015625と1.99999988079071044921875です)。この「隣の数」までの距離を1としたものがULP(*Unit in the last place*)です。

「浮動小数点の四則演算と平方根の演算の結果は無限精度で演算した場合と比較して0.5ULP以内になっていなければならない」

先ほどのこの精度に関する仕様は次のように読み替えることができます。

「浮動小数点で計算した加算、減算、乗算、除算、平方根の結果は、仮に無限精度浮動少数というものがあった場合の演算結果に最も近い近似値になっていなければならない」

これはかなり強力な仕様です。浮動小数点は四則演算と平方根に関してはベストを尽くしていると言っても過言ではありません。

区間演算

ここまでの話で

1.浮動小数点演算は計算がするたびに誤差が広がっていくこと
2.誤差の大きさには非常に強力な仕様があること

の二つがわかりました。浮動小数点である以上、演算結果の真の値を知ることはできませんが、精度が仕様で決められている演算に限れば、__真の値が取りうる上界と下界が計算できる__かもしれません。これを行うのが区間演算です。ここから先は実際に区間演算クラスErrFloatを作成していきます。

ErrFloat 1.「隣の数」を計算する

まずは基本的な操作として「隣の数」を計算できる必要があります。PBRT V3では自前で実装していますが、C++標準に同等の操作をする関数、std::nextafter()が用意されているのでこれを利用してみます。浮動小数点の「次の数」と「前の数」を得る関数は次のようになります。

float nextFloatUp(float v)
{
  return std::nextafter(v, (std::numeric_limits<float>::max)());
}
float nextFloatDown(float v)
{
  return std::nextafter(v, (std::numeric_limits<float>::lowest)());
}

ErrFloat 2.加算と減算

次に加算と減算を考えます。ここから先は演算の対象になる二つの数を $A$, $B$と置き、それらの値の真値がこの間にあることが確定している区間を $[Al,Ah]$,$[Bl,Bh]$とします。加算、$A+B$の区間は

$$ [Al+Bl,Ah+Bh] $$

であることは自明です。また減算$A-B$の区間も

$$ [Al-Bh,Al-Bh] $$

であることは自明です。

さてここに落とし穴があります。この加減算自体に誤差が含まれている__のです。この誤差に対して安全側に倒して、これらの__加算の度に常に区間を1ULPずつ大きくします。これは精度に関してベストを尽くしているとは言えませんが、実装の簡単さのためにこうします(PBR本では丸め考慮すると実行速度が非常に遅くなってしまうことにも言及しています)。コードは次のようになります。

ErrFlaot operator + (const ErrFlaot& other) const
{
    ErrFlaot r;
    r.value_ = value_ + other.value_;
    r.high_ = nextFloatUp(high_ + other.high_);
    r.low_ = nextFloatDown(low_ + other.low_);
    r.ref_ = ref_ + other.ref_;
    return r;
}
ErrFlaot operator - (const ErrFlaot& other) const
{
    ErrFlaot r;
    r.value_ = value_ - other.value_;
    r.high_ = nextFloatUp(high_ - other.low_);
    r.low_ = nextFloatDown(low_ - other.high_);
    r.ref_ = ref_ - other.ref_;
    return r;
}

ErrFloat 3.乗算

乗算$A*B$は加算、減算のように演算の結果の区間は自明ではありません。区間と0との関係で場合分けが必要です。全ての組み合わせを考えると次のテーブルの様になります。

区間の正負	inf	sup
$0<Al<Ah$,$0<Bl<Bh$	$Al*Bl$	$Ah*Bh$
$0<Al<Ah$,$Bl<0<Bh$	$Ah*Bl$	$Ah*Bh$
$Al<0<Ah$,$0<Bl<Bh$	$Al*Bh$	$Ah*Bh$
$Al<0<Ah$,$Bl<0<Bh$	$AhBl$ or $AlBh$	$AlBl$ or $AhBl$
$Al<Ah<0$,$Bl<0<Bh$	$Ah*Bh$	$Al*Bl$
$Al<0<Ah$,$Bl<Bh<0$	$Al*Bh$	$Al*Bl$
$Al<Ah<0$,$Bl<Bh<0$	$Al*Bh$	$Al*Bl$

これより、

$(AlBl,AhBl,AlBh,AhBh)$ のうち、最小のものが下限、最大のものが上限

を選択すればよさそうです。コードは次のようになります。

ErrFloat operator * (const ErrFloat& other) const
{
    const float v0 = high_ * other.high_;
    const float v1 = high_ * other.low_;
    const float v2 = low_ * other.high_;
    const float v3 = low_ * other.low_;
    ErrFloat r;
    r.value_ = value_ * other.value_;
    r.high_ = nextFloatUp(std::max(std::max(v0,v1), std::max(v2,v3)));
    r.low_ = nextFloatDown(std::min(std::max(v0,v1), std::min(v2, v3)));
    r.ref_ = ref_ * other.ref_;
    return r;
}

ErrFloat 4.除算

除算$A/B$も結果は自明ではなく、0を超えるか否かで場合分けが必要そうです。全ての組み合わせを考えると次のテーブルの様になります。

区間の正負	inf	sup
$0<Al<Ah$,$0<Bl<Bh$	$Al/Bh$	$Ah/Bl$
$0<Al<Ah$,$Bl<Bh<0$	$Ah/Bh$	$Ah/Bl$
$Al<0<Ah$,$0<Bl<Bh$	$Al/Bl$	$Ah/Bh$
$Al<0<Ah$,$Bl<Bh<0$	$Ah/Bl$	$Al/Bl$
$Al<Ah<0$,$Bl<Bh<0$	$Ah/Bl$	$Al/Bh$
$Bl<0<Bh$	-$\infty$	$\infty$

これより、

除数の区間が0をまたぐ場合は[$-\infty$,$+\infty$]
それ以外であれば$(Al/Bl,Al/Bh,Ah/Bl,Ah/Bh)$のうち、最小のものが下限、最大のものが上限

をそれぞれ選択すればいいことになります。コードにすると次のようになります。

ErrFloat operator / (const ErrFloat& other) const
{
    ErrFloat r;
    r.value_ = value_ / other.value_;
    r.ref_ = ref_ / other.ref_;
    if ((other.low_ <= 0.0f) &&
        (0.0f <= other.high_))
    {
        r.high_ = std::numeric_limits<float>::infinity();
        r.low_ = -std::numeric_limits<float>::infinity();
    }
    else
    {
        const float v0 = high_ / other.high_;
        const float v1 = high_ / other.low_;
        const float v2 = low_ / other.high_;
        const float v3 = low_ / other.low_;
        r.high_ = nextFloatUp(std::max(std::max(v0,v1), std::max(v2, v3)));
        r.low_ = nextFloatDown(std::min(std::min(v0, v1), std::min(v2, v3)));
    }
    return r;
}

ErrFloat 4.平方根

精度が保証されている最後の演算は平方根です。 $x^{\frac{1}{2}}$ は単調増加な関数なので単に区間で平方根を取るだけで完結します。コードは次の通りになります。

ErrFloat sqrt() const
{
    ErrFloat r;
    r.value_ = std::sqrtf(value_);
    r.low_ = nextFloatDown(std::sqrtf(low_));
    r.high_ = nextFloatUp(std::sqrtf(high_));
    return r;
}

ErrFloat 5. 二次方程式

最後に、球との交差判定のために二次方程式を追加します。ここで一つ泥臭いことをします。二次方程式の判別式を使いますが、この結果は誤差が広がりやすいです。球の交差判定では、この判別式のtrue/falseで球のエッジが確定します。実際にやってみるとこの誤差によるアーティファクトが気になる場合があります。このため二次方程式の判別式の部分だけ倍精度浮動小数点を使う事とします(PBRTのコードでも同様の事を行っています)。
※ またPBRTでは判別式を終えた後のDの値を再利用してなぜかエラーをリセットしていますが、真意はわかりません…

// 二次方程式の解(ErrFloat版)
bool solveQuadraticErrFloat(ErrFloat a, ErrFloat b, ErrFloat c, ErrFloat* t0, ErrFloat* t1)
{
    // 解の判定のみdoubleで行う
    const ErrFloat D = b * b - ErrFloat(4.0f) * a * c;
    const double Dhigh = double(b.value()) * double(b.value()) - 4.0 * (double)a.value() * double(c.value());
    // 解なし
    if (Dhigh < 0.0)
    {
        return false;
    }
#if 0 // PBRT版。真意はわからず。
    const double DsqrtTmp = std::sqrt(Dhigh);
    const float eps = std::numeric_limits<float>::epsilon() * DsqrtTmp;
    ErrFloat Dsqrt(float(DsqrtTmp), float(DsqrtTmp)-eps, float(DsqrtTmp)+eps);
#else
    const ErrFloat Dsqrt = D.sqrt();
#endif
    ErrFloat q;
    if (b.value() < 0.0f)
    {
        q = ErrFloat(-0.5f) * (b - Dsqrt);
    }
    else
    {
        q = ErrFloat(-0.5f) * (b + Dsqrt);
    }
    *t0 = q / a;
    *t1 = c / q;
    if (t1->value() < t0->value())
    {
        std::swap(*t0, *t1);
    }
    return true;
}

テスト

どの程度誤差が減るものなのかテストします。内容は次のようなものです。

単位球を空間上に置きます。
テスト1: 単位球の中心からレイを飛ばします。
テスト2: 単位球の中心から2のところから単位球の中心に向けてレイを飛ばします。
テスト1,2に関して原点付近から徐々に遠くに球を移動していきます。
レイの長さが1を超えたものは「めり込んだ」とし、誤りとします。

結果は以下のようになりました。

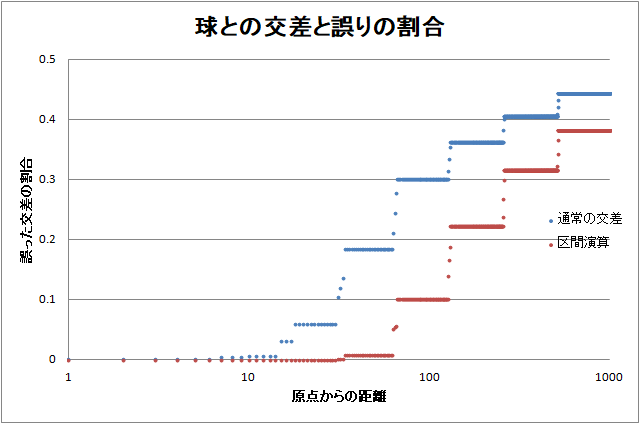
距離が伸びてくると区間演算版でも誤りが発生しだしますが、しばらく耐えていることがわかります。交差判定のインターフェイスにはErrFloatが出ていないので、区間演算を使っているバージョンでも誤った結果が出ます。

その他の話題

ErrFloatクラスのように浮動小数点演算をするたびに誤差を計算する方法は"Running error analysis“と呼ばれ、適用範囲が広い一方、実行効率がよくありません。行う処理によっては誤差の範囲を先に見積もることができます。詳しくはPBR本の”Error Propagation“の項を参照してください。
全く同じ意味の演算でも誤差が広がりやすい演算とそうでないものが存在します(例:悪性の相殺)。意味は変えずにエラーだけを最小化するように式を変形してくれるソフトウェアにHerbieというものがあります。
既存のコードをいじらなくても、レイとの交差判定は、__「二度打ち」__すると精度を上げることができます。つまり一度目の交差が終わったのちに、その交差点から少し手前から再度打ち直すことで交差判定処理の中に出てくる値を小さくすることができ、結果的に精度が上がります。
浮動小数点演算の誤差は扱う数値が大きくなればなるほど大きくなってきます。レイトレの文脈であれば__最初からカメラ座標を原点にしてオブジェクトを配置すれば誤差を抑えることができます__。

(引用: Matt Pharr’s blog|Rendering in Camera Space(ish) )

テストコード

#define _USE_MATH_DEFINES
#include <cmath>
#include <cstdio>
#include <cassert>
#include <cstdint>
//
#include <random>

//
float nextFloatUp(float v){ return std::nextafter(v, (std::numeric_limits<float>::max)()); }
//
float nextFloatDown(float v){ return std::nextafter(v, (std::numeric_limits<float>::lowest)()); }
//
class ErrFloat
{
public:
    ErrFloat() = default;
    ErrFloat(float v)
        :value_(v), high_(v), low_(v), ref_(v)
    {}
    ErrFloat(float v, float high, float low)
        :value_(v), high_(high), low_(low), ref_(v)
    {}
    ErrFloat(const ErrFloat& other)
        :value_(other.value_), high_(other.high_), low_(other.low_), ref_(other.ref_)
    {}
    ErrFloat operator + (const ErrFloat& other) const
    {
        ErrFloat r;
        r.value_ = value_ + other.value_;
        r.high_ = nextFloatUp(high_ + other.high_);
        r.low_ = nextFloatDown(low_ + other.low_);
        r.ref_ = ref_ + other.ref_;
        return r;
    }
    ErrFloat operator - (const ErrFloat& other) const
    {
        ErrFloat r;
        r.value_ = value_ - other.value_;
        r.high_ = nextFloatUp(high_ - other.low_);
        r.low_ = nextFloatDown(low_ - other.high_);
        r.ref_ = ref_ - other.ref_;
        return r;
    }
    ErrFloat operator * (const ErrFloat& other) const
    {
        const float v0 = high_ * other.high_;
        const float v1 = high_ * other.low_;
        const float v2 = low_ * other.high_;
        const float v3 = low_ * other.low_;
        ErrFloat r;
        r.value_ = value_ * other.value_;
        r.high_ = nextFloatUp(std::max(std::max(v0,v1), std::max(v2,v3)));
        r.low_ = nextFloatDown(std::min(std::max(v0,v1), std::min(v2, v3)));
        r.ref_ = ref_ * other.ref_;
        return r;
    }
    ErrFloat operator / (const ErrFloat& other) const
    {
        ErrFloat r;
        r.value_ = value_ / other.value_;
        r.ref_ = ref_ / other.ref_;
        if ((other.low_ <= 0.0f) &&
            (0.0f <= other.high_))
        {
            r.high_ = std::numeric_limits<float>::infinity();
            r.low_ = -std::numeric_limits<float>::infinity();
        }
        else
        {
            const float v0 = high_ / other.high_;
            const float v1 = high_ / other.low_;
            const float v2 = low_ / other.high_;
            const float v3 = low_ / other.low_;
            r.high_ = nextFloatUp(std::max(std::max(v0,v1), std::max(v2, v3)));
            r.low_ = nextFloatDown(std::min(std::min(v0, v1), std::min(v2, v3)));
        }
        return r;
    }
    ErrFloat sqrt() const
    {
        ErrFloat r;
        r.value_ = std::sqrtf(value_);
        r.low_ = nextFloatDown(std::sqrtf(low_));
        r.high_ = nextFloatUp(std::sqrtf(high_));
        return r;
    }
    float value() const
    {
        return value_;
    }
    float high() const
    {
        return high_;
    }
    float low() const
    {
        return low_;
    }
    void printAndCheck() const
    {
        if (std::isnan(value_))
        {
            return;
        }
        printf("V:%+10.10f, Int:[%+10.10f,%+10.10f]  Ref:%+10.10Lf\n", value_, low_, high_, ref_);
        assert((long double)(low_) <= ref_);
        assert(ref_ <= (long double)(high_));
    }
private:
    // 値
    float value_;
    // 区間
    float high_;
    float low_;
    // 真値
    long double ref_;
};

// 二次方程式の解(通常版)
bool solveQuadraticNaive(float a, float b, float c, float* t0, float* t1)
{
    const float D = b * b - 4.0f * a * c;
    if (D < 0.0)
    {
        return false;
    }
    const float Dsqrt = std::sqrtf(D);
    float q;
    if (float(b) < 0.0f)
    {
        q = -0.5f * (b - Dsqrt);
    }
    else
    {
        q = -0.5f * (b + Dsqrt);
    }
    *t0 = q / a;
    *t1 = c / q;
    if (*t1 < *t0)
    {
        std::swap(*t0, *t1);
    }
    return true;
}

// 二次方程式の解(ErrFloat版)
bool solveQuadraticErrFloat(ErrFloat a, ErrFloat b, ErrFloat c, ErrFloat* t0, ErrFloat* t1)
{
    // 解の判定のみdoubleで行う
    const ErrFloat D = b * b - ErrFloat(4.0f) * a * c;
    const double Dhigh = double(b.value()) * double(b.value()) - 4.0 * (double)a.value() * double(c.value());
    // 解なし
    if (Dhigh < 0.0)
    {
        return false;
    }
#if 0
    const double DsqrtTmp = std::sqrt(Dhigh);
    const float eps = std::numeric_limits<float>::epsilon() * 0.5f * DsqrtTmp;
    ErrFloat Dsqrt(float(DsqrtTmp), float(DsqrtTmp)-eps, float(DsqrtTmp)+eps);
#else
    const ErrFloat Dsqrt = D.sqrt();
#endif
    ErrFloat q;
    if (b.value() < 0.0f)
    {
        q = ErrFloat(-0.5f) * (b - Dsqrt);
    }
    else
    {
        q = ErrFloat(-0.5f) * (b + Dsqrt);
    }
    *t0 = q / a;
    *t1 = c / q;
    if (t1->value() < t0->value())
    {
        std::swap(*t0, *t1);
    }
    return true;
}

//
struct Vec3
{
public:
    float x;
    float y;
    float z;
    //
    Vec3 operator - (Vec3 other) const
    {
        Vec3 ret;
        ret.x = x - other.x;
        ret.y = y - other.y;
        ret.z = z - other.z;
        return ret;
    }
};

//
bool intersectSphereNaive(
    Vec3 org,
    Vec3 dir,
    Vec3 center,
    float radius,
    float* t)
{
    const Vec3 dif = org - center;
    const float ox(dif.x);
    const float oy(dif.y);
    const float oz(dif.z);
    const float dx(dir.x);
    const float dy(dir.y);
    const float dz(dir.z);
    const float r2 = radius * radius;
    const float a = dx * dx + dy * dy + dz * dz;
    const float b = 2 * (dx * ox + dy * oy + dz * oz);
    const float c = ox * ox + oy * oy + oz * oz - r2;
    //
    ErrFloat t0, t1;
    if (!solveQuadraticErrFloat(a, b, c, &t0, &t1))
    {
        return false;
    }
    //
    if (t1.low() <= 0.0f)
    {
        return false;
    }
    //
    ErrFloat rayt;
    if (t0.low() <= 0.0f)
    {
        rayt = t1;
    }
    else
    {
        rayt = t0;
    }
    // 安全側に倒す
    *t = float(rayt.low());
    //
    return true;
}

//
bool intersectSphereErrFloat(
    Vec3 org,
    Vec3 dir,
    Vec3 center,
    float radius,
    float* t)
{
    const ErrFloat orgx(org.x);
    const ErrFloat orgy(org.y);
    const ErrFloat orgz(org.z);
    const ErrFloat cx(center.x);
    const ErrFloat cy(center.y);
    const ErrFloat cz(center.z);
    const ErrFloat ox = orgx - cx;
    const ErrFloat oy = orgy - cy;
    const ErrFloat oz = orgz - cz;
    const ErrFloat dx(dir.x);
    const ErrFloat dy(dir.y);
    const ErrFloat dz(dir.z);
    const ErrFloat r2 = ErrFloat(radius) * ErrFloat(radius);
    const ErrFloat a = dx * dx + dy * dy + dz * dz;
    const ErrFloat b = ErrFloat(2.0f) * (dx * ox + dy * oy + dz * oz);
    const ErrFloat c = ox * ox + oy * oy + oz * oz - r2;
    //
    ErrFloat t0, t1;
    if (!solveQuadraticErrFloat(a, b, c, &t0, &t1))
    {
        return false;
    }
    //
    if (t1.low() <= 0.0f)
    {
        return false;
    }
    //
    ErrFloat rayt;
    if (t0.low() <= 0.0f)
    {
        rayt = t1;
    }
    else
    {
        rayt = t0;
    }
    // 安全側に倒す
    *t = float(rayt.low());
    //
    return true;
}

//
void test0()
{
    // テスト用の浮動小数を作成する
    const auto genTestFloat = [](int32_t index) -> float
    {
        switch (index)
        {
        case 0: return 0.0f;
        case 1: return -0.0f;
        case 2: return +1.0f;
        case 3: return -1.0f;
        case 4: return +1.000000001f;
        case 5: return -1.000000001f;
        case 6: return +2.000000000001f;
        case 7: return +100000.000000000001f;
        case 8: return +100000000.000000000001f;
        case 9: return -100000000.000000000001f;
        default:
        {
            std::mt19937 gen(index);
            for(int32_t i=0;i<128;++i){ gen();}
            std::uniform_real_distribution<float> dist(-1.0f, 1.0f);
            return dist(gen);
        }
        break;
        }
    };
    //
    const int32_t fi = 100;
    for(int32_t i=0;i<fi;++i)
    {
        for(int32_t j=0;j<fi;++j)
        {
            ErrFloat f0(genTestFloat(i));
            ErrFloat f1(genTestFloat(j));
            const auto e0 = f0 - f1;
            const auto e1 = f0 + f1;
            const auto e2 = f0 * f1;
            const auto e3 = f0 / f1;
            e0.printAndCheck();
            e1.printAndCheck();
            e2.printAndCheck();
            e3.printAndCheck();
        }
    }
}

//
void test1()
{
    //
    const auto testSphere = [](float dist)
    {
        const Vec3 testCenter = { dist,0.0f,0.0f };
        std::mt19937 rng(123);
        const int32_t numSample = 1024 * 4;
        int32_t invalidDistCountNaive = 0, invalidDistCountErrFloat = 0;
        int32_t invalidHitCountNaive = 0, invalidHitCountErrFloat = 0;
        for (int32_t sn = 0; sn < numSample; ++sn)
        {
            //
            const auto getSphere = [&]() ->Vec3
            {
                std::uniform_real_distribution<> dist(0.0, 1.0);
                const float u = float(dist(rng));
                const float v = float(dist(rng));
                const float z = 2.0f * u - 1.0f;
                const float theta = (2.0f * v - 1.0f) * float(M_PI);
                const float iz = sqrtf(1.0f - z * z);
                const float x = sinf(theta) * iz;
                const float y = cosf(theta) * iz;
                return Vec3{ x, y, z };
            };
            // テスト1
            {
                const Vec3 org = testCenter;
                const Vec3 dir = getSphere();
                const Vec3 center = org;
                const float radius = 1.0f;
                // 通常版
                {
                    float t = 0;
                    const bool hit = intersectSphereNaive(org, dir, center, radius, &t);
                    if (!hit)
                    {
                        ++invalidHitCountNaive;
                    }
                    if (t > 1.0f)
                    {
                        ++invalidDistCountNaive;
                    }
                }
                // ErrFloat版
                {
                    float t = 0;
                    const bool hit = intersectSphereErrFloat(org, dir, center, radius, &t);
                    if (!hit)
                    {
                        ++invalidHitCountErrFloat;
                    }
                    if (t > 1.0f)
                    {
                        ++invalidDistCountErrFloat;
                    }
                }
            }
            // テスト2
            {
                const Vec3 dir = getSphere();
                const Vec3 org =
                {
                    float(double(testCenter.x) - double(dir.x) * 2.0),
                    float(double(testCenter.y) - double(dir.y) * 2.0),
                    float(double(testCenter.z) - double(dir.z) * 2.0)
                };
                const Vec3 center = testCenter;
                const float radius = 1.0f;
                // 通常版
                {
                    float t = 0;
                    const bool hit = intersectSphereNaive(org, dir, center, radius, &t);
                    if (!hit)
                    {
                        ++invalidHitCountNaive;
                    }
                    if (t > 1.0f)
                    {
                        ++invalidDistCountNaive;
                    }
                }
                // ErrFloat版
                {
                    float t = 0;
                    const bool hit = intersectSphereErrFloat(org, dir, center, radius, &t);
                    if (!hit)
                    {
                        ++invalidHitCountErrFloat;
                    }
                    if (t > 1.0f)
                    {
                        ++invalidDistCountErrFloat;
                    }
                }
            }
        }
        printf("%f,%f,%f\n", dist, float(invalidDistCountNaive) / numSample, float(invalidDistCountErrFloat) / numSample);
    };
    testSphere(0.0f);
    for (float d = 1.0f; d < 1000.0f; d += 1.0f)
    {
        testSphere(d);
    }
}

//
int main()
{
    test0();
    test1();
    return 0;
}